Question

1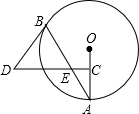．如图，AB是⊙O的弦，点C为半径OA的中点，过点C作CD⊥OA交弦AB于点E，连接BD，且DE=DB．
（1）判断BD与⊙O的位置关系，并说明理由；
（2）若CD=15，BE=10，tanA=$\frac{5}{12}$，求⊙O的直径．

Answer 1

分析 （1）连接OB，由圆的半径相等和已知条件证明∠OBD=90°，即可证明BD是⊙O的切线；
（2）过点D作DG⊥BE于G，根据等腰三角形的性质得到EG=$\frac{1}{2}$BE=5，由两角相等的三角形相似，△ACE∽△DGE，利用相似三角形对应角相等得到sin∠EDG=sinA=$\frac{5}{13}$，在Rt△EDG中，利用勾股定理求出DG的长，最后用三角函数即可得到结果．

解答 （1）证明：连接OB，
∵OB=OA，DE=DB，
∴∠A=∠OBA，∠DEB=∠ABD，
又∵CD⊥OA，
∴∠A+∠AEC=∠A+∠DEB=90°，
∴∠OBA+∠ABD=90°，
∴OB⊥BD，
∴BD是⊙O的切线；
（2）如图，过点D作DG⊥BE于G，

∵DE=DB，
∴EG=$\frac{1}{2}$BE=5，
∵∠ACE=∠DGE=90°，∠AEC=∠GED，
∴∠GDE=∠A，
∴△ACE∽△DGE，
∴sin∠EDG=sinA=$\frac{EG}{DE}$=$\frac{5}{13}$，即DE=13，
在Rt△ECG中，
∵DG=$\sqrt{D{E}^{2}-E{D}^{2}}$=12，
∵CD=15，DE=13，
∴CE=2，
在Rt△ACE中，AC=$\frac{CE}{tan∠A}$=$\frac{24}{5}$，
∴⊙O的直径2OA=4AC=$\frac{96}{5}$．

点评 此题考查了切线的判定，以及相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解本题的关键．