题目内容
19.已知关于x的一元二次方程x2-6x+m+4=0有两个实数根x1,x2.(1)求m的取值范围;
(2)若x1,x2满足3x1=|x2|+2,求m的值.
分析 (1)根据方程的系数结合根的判别式,即可得出△=20-4m≥0,解之即可得出结论;
(2)由根与系数的关系可得x1+x2=6①、x1•x2=m+4②,分x2≥0和x2<0可找出3x1=x2+2③或3x1=-x2+2④,联立①③或①④求出x1、x2的值,进而可求出m的值.
解答 解:(1)∵关于x的一元二次方程x2-6x+m+4=0有两个实数根x1,x2,
∴△=(-6)2-4(m+4)=20-4m≥0,
解得:m≤5,
∴m的取值范围为m≤5.
(2)∵关于x的一元二次方程x2-6x+m+4=0有两个实数根x1,x2,
∴x1+x2=6①,x1•x2=m+4②.
∵3x1=|x2|+2,
当x2≥0时,有3x1=x2+2③,
联立①③解得:x1=2,x2=4,
∴8=m+4,m=4;
当x2<0时,有3x1=-x2+2④,
联立①④解得:x1=-2,x2=8(不合题意,舍去).
∴符合条件的m的值为4.
点评 本题考查了根与系数的关系以及根的判别式,解题的关键是:(1)根据方程的系数结合根的判别式,找出△=20-4m≥0;(2)分x2≥0和x2<0两种情况求出x1、x2的值.

练习册系列答案
相关题目
10.化简$\frac{4x}{{x}^{2}-4}$-$\frac{x}{x-2}$的结果是( )
| A. | -x2+2x | B. | -x2+6x | C. | -$\frac{x}{x+2}$ | D. | $\frac{x}{x-2}$ |
14.下列计算正确的是( )
| A. | b3•b3=2b3 | B. | (a+2)(a-2)=a2-4 | ||
| C. | (ab2)3=ab6 | D. | (8a-7b)-(4a-5b)=4a-12b |
4.已知反比例函数y=$\frac{k}{x}$的图象过点A(1,-2),则k的值为( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
11.下列实数中最大的数是( )
| A. | 3 | B. | 0 | C. | $\sqrt{2}$ | D. | -4 |
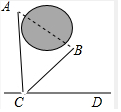 如图,A、B两个村庄之间有一个池塘,A村到公路CD的距离AC=700米,若BC═600米,∠BCD=30°,试求A、B两个村庄之间的距离(结果保留根号).
如图,A、B两个村庄之间有一个池塘,A村到公路CD的距离AC=700米,若BC═600米,∠BCD=30°,试求A、B两个村庄之间的距离(结果保留根号).