��Ŀ����
14��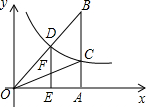 ��֪����ͼ������������y=ax��ͼ���뷴��������y=$\frac{k}{x}$��ͼ���ڵ�C��3��1��
��֪����ͼ������������y=ax��ͼ���뷴��������y=$\frac{k}{x}$��ͼ���ڵ�C��3��1����1����ȷ���������������ͷ����������ı���ʽ��
��2������ͼ��ش��ڵ�һ�����ڣ���xȡ��ֵʱ��������������ֵ����������������ֵ��
��3����D��m��n���Ƿ���������ͼ���ϵ�һ���㣬����0��m��3������C��ֱ��AC��x���ڵ�A����OD���ӳ����ڵ�B������D��OB���е㣬DE��x���ڵ�E����OC�ڵ�F�������ı���DFCB�������
���� ��1������C��3��1���ֱ����y=$\frac{k}{x}$��y=ax���k��a���ɵã�
��2������ͼ���ҵ�����������ͼ��������������ͼ���Ϸ���Ӧ��x��ȡֵ��Χ��
��3�����ݵ�DΪOB�е㡢���ڷ����������ϣ����DE��OA������λ�߶����ɵõ�D��B���꣬����õ�F���꣬�Ӷ���DF=$\frac{3}{2}$��BC=3��EA=$\frac{3}{2}$���ݴ˿ɵô𰸣�
��� �⣺��1������C��3��1���ֱ����y=$\frac{k}{x}$��y=ax���ã�k=3��a=$\frac{1}{3}$��
�෴������������ʽΪy=$\frac{3}{x}$����������������ʽΪy=$\frac{1}{3}$x��
��2���۲�ͼ���֪���ڵڶ������ڣ���0��x��3ʱ������������ֵ��������������ֵ��
��3���ߵ�D��m��n����OB���е㣬���ڷ���������y=$\frac{3}{x}$�ϣ�
��OE=$\frac{1}{2}$OA=$\frac{3}{2}$����D��$\frac{3}{2}$��2����
���B��3��4����
�֡ߵ�F������������y=$\frac{1}{3}$xͼ���ϣ�
��F��$\frac{3}{2}$��$\frac{1}{2}$����
��DF=$\frac{3}{2}$��BC=3��EA=$\frac{3}{2}$��
���ı���DFCB�����Ϊ$\frac{1}{2}$����$\frac{3}{2}$+3����$\frac{3}{2}$=$\frac{27}{8}$��
���� ���⿼����һ�κ����뷴���������Ľ������⣬�����˴���ϵ����������ϵ��������ѧ����Ҫ��˼�뷽����ѧ��ע��������ã�

| A�� | 3 | B�� | 0 | C�� | $\sqrt{2}$ | D�� | -4 |
| A�� | x2+8x+16 | B�� | x2+8x+8 | C�� | x2+16 | D�� | x2-4x+16 |
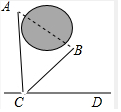 ��ͼ��A��B������ׯ֮����һ��������A�嵽��·CD�ľ���AC=700�ף���BC�T600�ף���BCD=30�㣬����A��B������ׯ֮��ľ��루����������ţ���
��ͼ��A��B������ׯ֮����һ��������A�嵽��·CD�ľ���AC=700�ף���BC�T600�ף���BCD=30�㣬����A��B������ׯ֮��ľ��루����������ţ���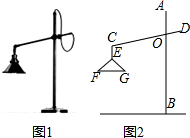 ��ͼ1��ʾ����һ�����������ϵļ���̨�ƣ�����ṹ��ͼ2���Ƹ�AB��CD���ڵ�O����O�̶�������������CEʼ�ձ�����ABƽ�У������·�FG����ˮƽλ�ã����OC=20cm����COB=70�㣬��F=40�㣬EF=EG����G��OB�ľ���Ϊ14cm��
��ͼ1��ʾ����һ�����������ϵļ���̨�ƣ�����ṹ��ͼ2���Ƹ�AB��CD���ڵ�O����O�̶�������������CEʼ�ձ�����ABƽ�У������·�FG����ˮƽλ�ã����OC=20cm����COB=70�㣬��F=40�㣬EF=EG����G��OB�ľ���Ϊ14cm��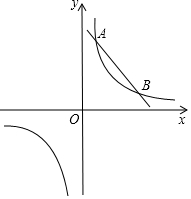 ��ͼ��ֱ��y=-x+b�뷴��������y=$\frac{k}{x}$��ͼ�ν���A��a��4����B��4��1�����㣮
��ͼ��ֱ��y=-x+b�뷴��������y=$\frac{k}{x}$��ͼ�ν���A��a��4����B��4��1�����㣮 ��ͼ����֪��ABC�У�AB=AC���ѡ�ABC��A����˳ʱ�뷽����ת�õ���ADE������BD��CE���ڵ�F��
��ͼ����֪��ABC�У�AB=AC���ѡ�ABC��A����˳ʱ�뷽����ת�õ���ADE������BD��CE���ڵ�F��