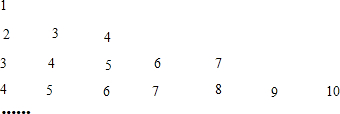题目内容
20.解下列不等式,并把它们的解集分别表示在数轴上:(1)3x-2x<5;
(2)x-6>2x;
(3)$\frac{x}{2}$>$\frac{x}{3}$;
(4)2x-7>5-2x;
(5)$\frac{1-3x}{2}$>1-2x;
(6)x-$\frac{1}{2}$(4x-1)≤2;
(7)$\frac{x-1}{2}$+1≥$\frac{x}{4}$;
(8)0.01x-1≤0.02x.
分析 根据一元一次不等式的解法分别求解即可,再依据:“大于向右、小于向左、包括用实心点、不包括用空心点“在数轴上表示解集.
解答 解:(1)合并,得:x<5;
在数轴上表示不等式解集如图:
(2)移项、合并,得:-x>6,
系数化为1,得:x<-6;
在数轴上表示不等式解集如图:
(3)去分母,得:3x>2x,
移项、合并,得:x>0;
在数轴上表示不等式解集如图:
(4)移项、合并,得:4x>12,
系数化为1,得:x>3;
在数轴上表示不等式解集如图:
(5)去分母,得:1-3x>2-4x,
移项,得:-3x+4x>2-1,
合并,得:x>1;
在数轴上表示不等式解集如图:
(6)去括号,得:x-2x+$\frac{1}{2}$≤2,
移项、合并,得:-x≤$\frac{3}{2}$,
系数化为1,得:x≥-$\frac{3}{2}$;
在数轴上表示不等式解集如图:
(7)去分母,得:2(x-1)+4≥x,
去括号,得:2x-2+4≥x,
移项、合并,得:x≥-2;
在数轴上表示不等式解集如图:
(8)移项、合并,得:-0.01x≤1,
系数化为1,得:x≥100,
在数轴上表示不等式解集如图:
点评 本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.也考查了在数轴上表示不等式的解集.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.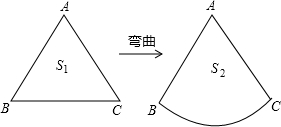 如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )
如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )
 如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )
如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )| A. | S1<S2 | B. | S1=S2 | C. | S1>S2 | D. | 无法确定 |
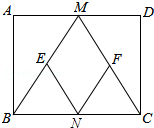 已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.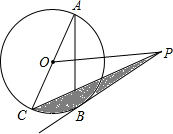 已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点.∠PBA=∠ACB.
已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点.∠PBA=∠ACB. 如图:已知DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°
如图:已知DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°