题目内容
17.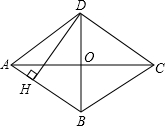 如图所示,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB 于点H,且DH与AC交于点G,则AH的长是多少?
如图所示,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB 于点H,且DH与AC交于点G,则AH的长是多少?
分析 根据菱形的面积等于对角线积的一半,可求得菱形的面积,又由菱形的对角线互相平分且垂直,可根据勾股定理得AB的长,根据菱形的面积的求解方法:底乘以高或对角线积的一半,即可得菱形的高,再利用勾股定理得出AH的长.
解答 解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=$\frac{1}{2}$AC=4cm,OB=OD=3cm,
∴AB=5cm,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=AB•DH,
∴DH=$\frac{AC×BD}{2AB}$=$\frac{24}{5}$(cm),
∴AH=$\sqrt{A{D}^{2}-D{H}^{2}}$=$\frac{7}{5}$(cm).
点评 此题考查了菱形的性质:菱形的对角线互相平分且垂直;菱形的面积的求解方法:底乘以高或对角线积的一半等知识,得出DH的长是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.下列实数中,无理数是( )
| A. | -$\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{9}$ | D. | -|-5| |
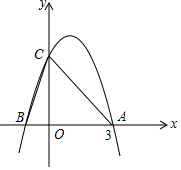 如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.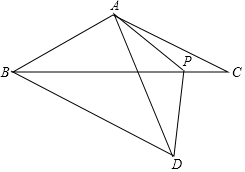 如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4.
如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4.