Question

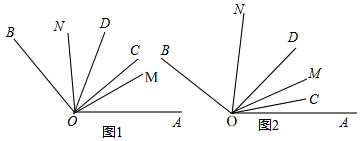
12．（1）如图1，射线OC、OD在∠AOB的内部，射线OM、ON分别平分∠AOD、∠BOC、且∠BON=50°，∠AOM=40°，∠COD=30°，求∠AOB的度数；
（2）如图2，射线OC、OD在∠AOB的内部，射线OM、ON分别平分∠AOD、∠BOC、且∠AOB=150°，∠COD=30°，求∠MON的度数．

Answer 1

分析 （1）根据角平分线的定义可得出∠AOD、∠BOC的度数，结合∠AOB=∠AOD-∠COD+∠BOC即可得出结论；
（2）根据角平分线的定义可得出∠AOM=$\frac{1}{2}$∠AOD、∠BON=$\frac{1}{2}$∠BOC，由∠AOB=150°、∠COD=30°即可算出∠AOD+∠BOC的度数，再根据∠MON=∠AOB-$\frac{1}{2}$（∠AOD+∠BOC），代入数据即可得出结论．

解答 解：（1）∵射线OM、ON分别平分∠AOD、∠BOC，且∠BON=50°，∠AOM=40°，
∴∠AOD=2∠AOM=80°，∠BOC=2∠BON=100°，
∵∠COD=30°，
∴∠AOB=∠AOD-∠COD+∠BOC=80°-30°+100°=150°．
（2）∵射线OM、ON分别平分∠AOD、∠BOC，
∴∠AOM=$\frac{1}{2}$∠AOD，∠BON=$\frac{1}{2}$∠BOC，
∵∠AOB=150°，∠COD=30°，
∴∠AOD+∠BOC=∠AOB+∠COD=150°+30°=180°，
∴∠MON=∠AOB-（∠BON+∠AOM）=∠AOB-$\frac{1}{2}$（∠AOD+∠BOC）=150°-90°=60°．

点评 本题考查了角的有关计算和角平分线定义的应用，能表示出各个角之间的关系是解此题的关键．