题目内容
17．
如图，已知△ABC的三个顶点分别为A（2，3）、B（3，1）、C（-2，-2）．（1）请在图中画出△ABC关于y轴的轴对称图形△DEF（A、B、C的对应点分别是D、E、F），并直写出D、E、F的坐标．
（2）求四边形ABED的面积．
分析 （1）分别画出A、B、C三点关于y轴的对称点D、E、F即可解决问题．
（2）四边形ABED是等腰梯形，根据梯形的面积公式即可解决问题．
解答 解：（1）△ABC关于y轴的轴对称图形△DEF如图所示，
由图象可知：D（-2，3）、E（-3，1）、F（2，-2），
（2）S梯形ABED=$\frac{1}{2}$•（4+6）•2=10．
点评 本题考查作图-轴对称变换，梯形的面积公式等知识，解题的关键是学会作对称图形，记住梯形的面积公式，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC中，∠BAC=90°，AB=AC，F是BC上一点，BD⊥AF交AF的延长线于D，CE⊥AF于E，求证：ED=CE-BD．
5．
如图，在△ABC中，∠ABC=90°，∠A=30°，BC=1．M、N分别是AB、AC上的任意一点，求MN+NB的最小值为（ ）
如图，在△ABC中，∠ABC=90°，∠A=30°，BC=1．M、N分别是AB、AC上的任意一点，求MN+NB的最小值为（ ）| A． | 1.5 | B． | 2 | C． | $\frac{{\sqrt{3}}}{2}$+$\frac{3}{4}$ | D． | $\sqrt{3}$ |
2．下列说法不正确的是（ ）
| A． | 0的平方根是0 | B． | 40的算术平方根是20 | ||
| C． | -1的立方根是-1 | D． | $\sqrt{10}$是10的平方根 |
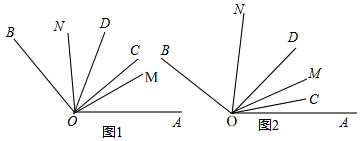
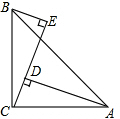如图，△ABC中，∠ACB=90°，AC=BC，BE⊥CE，AD⊥CE，垂足分别为E和D．试猜想线段AD、BE、DE三者之间有何数量关系？并证明你的猜想．