Question

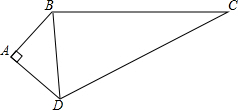如图，已知AB=3，BC=12，CD=13，DA=4，求四边形ABCD的面积．

Answer 1

考点：勾股定理,勾股定理的逆定理

专题：计算题

分析：利用勾股定理列式求出BD，再利用勾股定理逆定理判断出△BCD是直角三角形，然后根据S_{四边形ABCD}=S_△ABD+S_△BCD列式计算即可得解．

解答：解：由勾股定理得，BD=

AB2+AD2

=

32+42

=5，
∵BD²+BC²=5²+12²=169=CD²，
∴△BCD是直角三角形，∠DBC=90°，
∴S_{四边形ABCD}=S_△ABD+S_△BCD，
=

1

2

×3×4+

1

2

×12×5，
=6+30，
=36．

点评：本题考查了勾股定理，勾股定理逆定理，熟记两个定理并判断出△BCD是直角三角形是解题的关键．