题目内容
如图，AB∥CD，试求∠BAP、∠APC、∠PCD三者间的关系式，并进行严格的证明．考点：平行线的性质
专题：探究型
分析：作PE∥AB，由AB∥CD，根据平行线的性质得PE∥CD，∠1=∠BAP，则∠2=∠DCP，于是有∠BAP+∠PCD=∠APC．
解答：
解：∠BAP+∠PCD=∠APC．理由如下：
作PE∥AB，如图，
∵AB∥CD，
∴PE∥CD，∠1=∠BAP，
∴∠2=∠DCP，
∴∠1+∠2=∠BAP+∠DCP，
即∠BAP+∠PCD=∠APC．
解：∠BAP+∠PCD=∠APC．理由如下：作PE∥AB，如图，
∵AB∥CD，
∴PE∥CD，∠1=∠BAP，
∴∠2=∠DCP，
∴∠1+∠2=∠BAP+∠DCP，
即∠BAP+∠PCD=∠APC．
点评：本题考查了平行线的性质：两直线平行，内错角相等．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知：如图，CD平分∠ACB，CD∥AE．求证：CA=CE．（请写出只要证明依据）
如图，平行四边形ABCD的对角线AC、BD交于点O，AC⊥AB，AB=
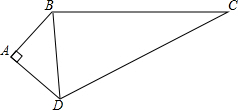如图，已知AB=3，BC=12，CD=13，DA=4，求四边形ABCD的面积．