题目内容
已知关于x的一元二次方程x2-2x+m=0
(1)当m=4时,判断方程的根的情况;
(2)当m=-3时,求方程的根.
(1)当m=4时,判断方程的根的情况;
(2)当m=-3时,求方程的根.
考点:根的判别式,解一元二次方程-因式分解法
专题:计算题,判别式法
分析:(1)当m=4时,方程可得x2-2x+4=0,再根据△=b2-4ac,判断出△的情况,即可得出该方程的根的情况;
(2)把m=-3得出x2-2x+m=0,得出x2-2x-3=0,再进行整理,即可求出方程的根.
(2)把m=-3得出x2-2x+m=0,得出x2-2x-3=0,再进行整理,即可求出方程的根.
解答:解:(1)∵一元二次方程x2-2x+m=0,
∴m=4时方程可变为:x2-2x+4=0,
∴△=b2-4ac=(-2)2-4×1×4=4-16=-12<0,
∴当m=4时,方程没有实数根;
(2)当m=-3时,方程可得为:x2-2x-3=0,
整理得:(x-3)(x+1)=0,
解得:x1=3,x2=-1.
故答案为:(1)没有实数根;(2)3和-1.
∴m=4时方程可变为:x2-2x+4=0,
∴△=b2-4ac=(-2)2-4×1×4=4-16=-12<0,
∴当m=4时,方程没有实数根;
(2)当m=-3时,方程可得为:x2-2x-3=0,
整理得:(x-3)(x+1)=0,
解得:x1=3,x2=-1.
故答案为:(1)没有实数根;(2)3和-1.
点评:此题考查了根的判别式和因式分解法解一元二次方程,掌握一元二次方程根的情况与判别式△的关系:△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根是本题的关键.

练习册系列答案
相关题目
点P(3,-1)在第( )象限.
| A、一 | B、二 | C、三 | D、四 |
 已知:如图,CD平分∠ACB,CD∥AE.求证:CA=CE.(请写出只要证明依据)
已知:如图,CD平分∠ACB,CD∥AE.求证:CA=CE.(请写出只要证明依据)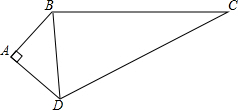 如图,已知AB=3,BC=12,CD=13,DA=4,求四边形ABCD的面积.
如图,已知AB=3,BC=12,CD=13,DA=4,求四边形ABCD的面积.