题目内容
计算:
(1)25×5×52-52×53;
(2)an+1•a3+an•a4;
(3)-a2•(-a)3•a+a4•(-a)2.
(1)25×5×52-52×53;
(2)an+1•a3+an•a4;
(3)-a2•(-a)3•a+a4•(-a)2.
考点:同底数幂的乘法,幂的乘方与积的乘方
专题:
分析:(1)直接利用同底数幂的乘法运算法则化简,进而合并求出即可;
(2)直接利用同底数幂的乘法运算法则化简,进而合并求出即可;
(3)直接利用同底数幂的乘法运算法则化简,进而合并求出即可.
(2)直接利用同底数幂的乘法运算法则化简,进而合并求出即可;
(3)直接利用同底数幂的乘法运算法则化简,进而合并求出即可.
解答:解:(1)25×5×52-52×53
=52×5×52-52×53
=55-55
=0;
(2)an+1•a3+an•a4
=an+4+an+4
=2an+4;
(3)-a2•(-a)3•a+a4•(-a)2
=-a6+a6
=0.
=52×5×52-52×53
=55-55
=0;
(2)an+1•a3+an•a4
=an+4+an+4
=2an+4;
(3)-a2•(-a)3•a+a4•(-a)2
=-a6+a6
=0.
点评:此题主要考查了同底数幂的乘法运算,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
分式-
可化简为( )
| a+b |
| (a-b)(a+b) |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
 如图所示,已知直线y=-
如图所示,已知直线y=-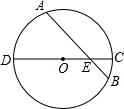 如图,CD为⊙O的直径,弦AB交CD于点E,∠CEB=45°,DE=9cm,CE=3cm,求弦AB的长.
如图,CD为⊙O的直径,弦AB交CD于点E,∠CEB=45°,DE=9cm,CE=3cm,求弦AB的长.