题目内容
(1)如图,已知∠AOB,请你利用图①,用尺规作出∠AOB的平分线0P,并画一对以OP所在直线为对称轴的全等三角形;
(2)参考(1)中画全等三角形的方法,解答下列问题:如图②,在ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC与∠BCA的平分线,AD和CE相交于点F,请猜想FE与FD有怎样的数量关系,并加以说明.
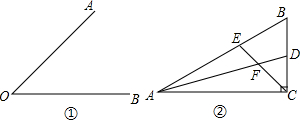
(2)参考(1)中画全等三角形的方法,解答下列问题:如图②,在ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC与∠BCA的平分线,AD和CE相交于点F,请猜想FE与FD有怎样的数量关系,并加以说明.

考点:作图-轴对称变换,全等三角形的判定与性质
专题:
分析:(1)作图略在OA和OB上截取OE=OF,在OP上任取一点C,连接CE、CF,则△COE≌△COF;
(2)在AC上截取AM=AE,连接MF,根据AD是∠BAC的平分线可得出∠EAF=∠MAF,EF=MF.再由CE是∠BCA的平分线可知∠ACB=90°,∠DCF=45°.根据全等三角形的判定定理得出△CDF≌△CMF,由此可得出结论.
(2)在AC上截取AM=AE,连接MF,根据AD是∠BAC的平分线可得出∠EAF=∠MAF,EF=MF.再由CE是∠BCA的平分线可知∠ACB=90°,∠DCF=45°.根据全等三角形的判定定理得出△CDF≌△CMF,由此可得出结论.
解答: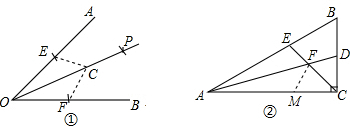 解:(1)如图①所示;
解:(1)如图①所示;
(2)FE=FD.
如图②,在AC上截取AM=AE,连接MF,
∵AD是∠BAC的平分线,
∴∠EAF=∠MAF,
在△AEF与△AMF中,
,
∴△AEF≌△AMF(SAS).
∴EF=MF.
∵CE是∠BCA的平分线,∠ACB=90°,
∴∠DCF=45°.
又∵∠B=60°,
∴∠CAD=15°,
∴∠CDF=75°,
∴∠AMF=∠AEF=105°,
∴∠FMC=75°,∠CDF=∠CMF.
在△CDF与△CMF中,
,
∴△CDF≌△CMF(AAS),
∴FD=FM,
∴EF=DF.
 解:(1)如图①所示;
解:(1)如图①所示;(2)FE=FD.
如图②,在AC上截取AM=AE,连接MF,
∵AD是∠BAC的平分线,
∴∠EAF=∠MAF,
在△AEF与△AMF中,
|
∴△AEF≌△AMF(SAS).
∴EF=MF.
∵CE是∠BCA的平分线,∠ACB=90°,
∴∠DCF=45°.
又∵∠B=60°,
∴∠CAD=15°,
∴∠CDF=75°,
∴∠AMF=∠AEF=105°,
∴∠FMC=75°,∠CDF=∠CMF.
在△CDF与△CMF中,
|
∴△CDF≌△CMF(AAS),
∴FD=FM,
∴EF=DF.
点评:本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
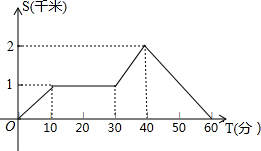 星期天晚饭后,小丽的爸爸从家里出去散步,如图描述了她爸爸散步过程中离家的距离(km)与散步所用的时间(min)之间的函数关系,依据图象,下面描述符合小丽爸爸散步情景的是( )
星期天晚饭后,小丽的爸爸从家里出去散步,如图描述了她爸爸散步过程中离家的距离(km)与散步所用的时间(min)之间的函数关系,依据图象,下面描述符合小丽爸爸散步情景的是( )| A、从家出发,休息一会,就回家 |
| B、从家出发,一直散步(没有停留),然后回家 |
| C、从家出发,休息一会,返回用时20分钟 |
| D、从家出发,休息一会,继续行走一段,然后回家 |
下面各式正确的是( )
A、
| ||
B、±
| ||
C、-
| ||
D、-
|
下列图形中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
在平面直角坐标系中,点(3,-5)关于x轴的对称点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
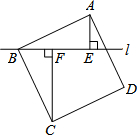 如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=5,CF=12,则AB的长为
如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=5,CF=12,则AB的长为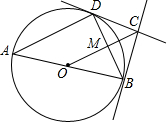 如图,AB为⊙O的直径,BC⊥AB,OC过BD中点M,求证:CD是⊙O的切线.
如图,AB为⊙O的直径,BC⊥AB,OC过BD中点M,求证:CD是⊙O的切线.