题目内容
3.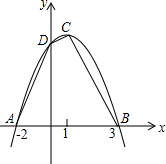 已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.(1)求二次函数的解析式;
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
分析 (1)根据函数图象过点(-2,0)和(4,0)可得对称轴为x=1,又函数的最大值为9,则顶点的纵坐标为9,所以可设y=a(x-1)2+9,再把点B的坐标代入求出a的值即可;
(2)过C作CE⊥x轴于E点,根据点的坐标求得两个三角形的面积和一个梯形的面积,它们的和就是四边形ABCD的面积.
解答 解:(1)由抛物线的对称性知,它的对称轴是x=1.
又∵函数的最大值为9,
∴抛物线的顶点为C(1,9).
设抛物线的解析式为y=a(x-1)2+9,代入B(4,0),求得a=-1.
∴二次函数的解析式是y=-(x-1)2+9,
即y=-x2+2x+8.
(2)过C作CE⊥x轴于E点.
当x=0时,y=8,即抛物线与y轴的交点坐标为D(0,8).
∴S四边形ABCD=S△AOD+S四边形DOEC+S△BCE=$\frac{1}{2}$×2×8+$\frac{1}{2}$×(8+9)×1+$\frac{1}{2}$×2×9=25.5.
点评 本题考查了待定系数法,抛物线和坐标轴的交点、顶点坐标,四边形的面积的求法等,(2)利用分割法求四边形的面积是本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
14.下列不等式解法正确的是( )
| A. | 如果-$\frac{1}{2}$x>2,那么x<-1 | B. | 如果$\frac{3}{2}$x>-$\frac{2}{3}$,那么x>-1 | ||
| C. | 如果3x<-3,那么x>-1 | D. | 如果-$\frac{11}{3}$x<0,那么x>0 |
 如图,正方形网格中每个小正方形的边长都是1,△ABC的三个顶点A、B、C都是格点(每个小正方形的顶点叫做格点).
如图,正方形网格中每个小正方形的边长都是1,△ABC的三个顶点A、B、C都是格点(每个小正方形的顶点叫做格点).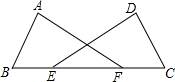 已知:BE=CF,AB=CD,∠B=∠C.求证:AF=DE.
已知:BE=CF,AB=CD,∠B=∠C.求证:AF=DE.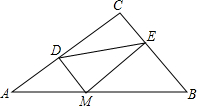 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为$\frac{12}{5}$.
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为$\frac{12}{5}$. 如图所示的几何体是由16个棱长为1厘米的小正方体堆积而成的,问这个几何体的表面积是多少平方厘米?
如图所示的几何体是由16个棱长为1厘米的小正方体堆积而成的,问这个几何体的表面积是多少平方厘米?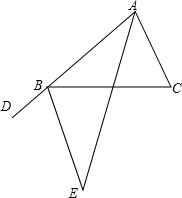 完成下面证明:如图,B是射线AD上一点,AE平分∠DAC,∠DAC=∠C=∠CBE
完成下面证明:如图,B是射线AD上一点,AE平分∠DAC,∠DAC=∠C=∠CBE