题目内容
5.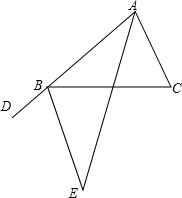 完成下面证明:如图,B是射线AD上一点,AE平分∠DAC,∠DAC=∠C=∠CBE
完成下面证明:如图,B是射线AD上一点,AE平分∠DAC,∠DAC=∠C=∠CBE(1)求证:BE平分∠DBC
证明:∵∠C=∠CBE(已知)
∴BE∥AC(内错角相等,两直线平行)
∴∠DBE=∠DAC(两直线平行,同位角相等)
∵∠DAC=∠C(已知)
∴∠DBE=∠CBE(等量代换)
∴BE平分∠DBC(角平分线定义)
(2)请模仿(1)的证明过程,尝试证明∠E=∠BAE.
分析 (1)由内错角相等得出BE∥AC,得出同位角相等,由已知条件得出∠DBE=∠CBE,即可得出结论;
(2)由内错角相等得出BE∥AC,得出同位角相等,由已知条件得出∠BAE=∠CAE,即可得出结论.
解答 (1)证明:∵∠C=∠CBE(已知)
∴BE∥AC(内错角相等,两直线平行 )
∴∠DBE=∠DAC(两直线平行,同位角相等 )
∵∠DAC=∠C(已知)
∴∠DBE=∠CBE(等量代换 )
∴BE平分∠DBC(角平分线定义 );
故答案为:内错角相等,两直线平行;两直线平行,同位角相等;等量代换;角平分线定义;
(2)证明:∵∠C=∠CBE(已知)
∴BE∥AC(内错角相等,两直线平行 )
∴∠E=∠CAE(两直线平行,同位角相等 )
∵AE平分∠DAC(已知),
∴∠BAE=∠CAE(角平分线定义,
∴∠E=∠BAE(等量代换).
点评 本题考查了平行线的判定与性质、角平分线的定义;熟练掌握平行线的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9. 如图,在△ABC中,∠A=45°,∠B=120°,AB=6,求BC的长(结果精确到0.1).
如图,在△ABC中,∠A=45°,∠B=120°,AB=6,求BC的长(结果精确到0.1). 已知:抛物线C1:y=x2-2x-3.
已知:抛物线C1:y=x2-2x-3. 如图,在△ABC中,AC=4,AB=5,BC=6,点D、E分别在AB、AC上,且∠AED=∠B,如果四边形BCED的周长为13,求DE的长.
如图,在△ABC中,AC=4,AB=5,BC=6,点D、E分别在AB、AC上,且∠AED=∠B,如果四边形BCED的周长为13,求DE的长.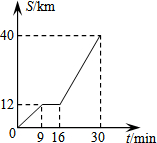 如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题: 如图是一个4×4的正方形网格,图中所标示的7个角的角度之和等于585°.
如图是一个4×4的正方形网格,图中所标示的7个角的角度之和等于585°.