题目内容
19.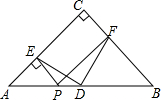 △ABC中,∠C=90°,BC=AC,D为AB中点,P是AB上一点,PE⊥AC于E,PF⊥BC于F.
△ABC中,∠C=90°,BC=AC,D为AB中点,P是AB上一点,PE⊥AC于E,PF⊥BC于F.(1)求证:DE=DF且DE⊥DF;
(2)若P是AB延长线上一点,其它条件不变,(1)中的结论是否仍然成立,给予结论并画图证明.
分析 (1)根据等腰直角三角形的性质得出∠A=∠DCF=45°,再利用SAS证明△AED与△DCF全等,进而得出答案;
(2)根据等腰直角三角形的性质得出∠DCE=∠DBF,再利用SAS证明△DCE与△DBF全等,进而得出答案.
解答 证明:(1)连接CD,如图1: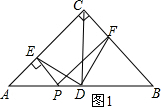
∵△ABC中,∠C=90°,BC=AC,D为AB中点,
∴CD=AD=DB,CD⊥AB,∠A=∠DCF=45°,
∵PE⊥AC于E,PF⊥BC于F,∠C=90°,
∴PE=CF=AE,
在△AED与△DCF中,
$\left\{\begin{array}{l}{AE=CF}\\{∠A=∠DCF}\\{AD=CD}\end{array}\right.$,
∴△AED≌△DCF(SAS),
∴DE=DF,∠ADE=∠CDF,
∵∠ADE+∠EDC=90°,
∴∠CDF+∠EDC=90°,
∴DF⊥DE;
(2)连接CD,如图2: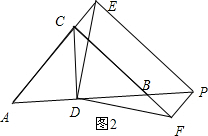
∵△ABC中,∠C=90°,BC=AC,D为AB中点,
∴CD=AD=DB,CD⊥AB,∠ABC=∠DCB=45°,
∵PE⊥AC于E,PF⊥BC于F,∠C=90°,
∴PF=CE=BF,
∵∠DCE=90°+45°=135°,∠DBF=180°-45°=135°,
∴∠DCE=∠DBF,
在△DCE与△DBF中,
$\left\{\begin{array}{l}{CD=DB}\\{∠DCE=∠DBF}\\{CE=BF}\end{array}\right.$,
∴△DCE≌△DBF(SAS),
∴DE=DF,∠CDE=∠BDF,
∵∠CDE+∠EDB=90°,
∴∠BDF+∠EDB=90°,
∴DF⊥DE.
点评 此题考查全等三角形的判定和性质,关键是根据SAS证明△AED与△DCF全等.

练习册系列答案
相关题目
9.若关于x的方程x2-2x+a=3的解为x=-2,则字母a的值为( )
| A. | 3 | B. | 5 | C. | -5 | D. | 11 |
10. 如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )
如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )
 如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )
如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )| A. | 1:2 | B. | 1:3 | C. | 2:1 | D. | 2:3 |
4.某厂要招聘A,B两个工种的工人共100人,根据工作需要,要求A工种的人数不少B工种人数的$\frac{3}{2}$倍,那么A,B两个工种的月工资如表时,招聘A工种几人才能使这100人每月所付的工资最少?
| 工种 | A | B |
| 月收入(元/人) | 3600 | 1800 |
11.正六边形的边心距是$\sqrt{3}$,则它的边长是( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
9.图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=-$\frac{1}{400}$(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为( )
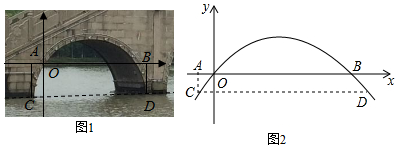

| A. | 16$\frac{9}{40}$米 | B. | $\frac{17}{4}$米 | C. | 16$\frac{7}{40}$米 | D. | $\frac{15}{4}$米 |
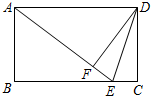 如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.
如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.
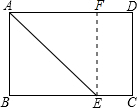 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm.
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm.