题目内容
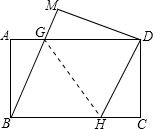 如图,在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿GH折叠,使点B与D重合,则下列语句正确的是( )
如图,在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿GH折叠,使点B与D重合,则下列语句正确的是( )①四边形BGDH是菱形;
②AG=1.75;
③GH=7.5;
④四边形BGDH的面积是37.5.
| A、只有①② | B、只有②③ |
| C、①②③ | D、①②③④ |
考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线求出BD的长度;根据题意证明四边形BGDH是菱形;根据勾股定理求出AG的长度;进而求出该菱形的面积;求出GH的长度即可解决问题.
解答: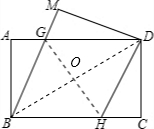 解:连接BD交GH于点O;
解:连接BD交GH于点O;
由题意得:GB=GD,BO=DO,BD⊥GH;
∵四边形ABCD为矩形,
∴∠C=90°,DC=AB=6,DG∥BC;
由勾股定理得:BD2=BC2+DC2=64+36=100,
∴BD=10;
∵DG∥BC,
∴∠DGO=∠BHO;
在△DGO与△BHO中,
,
∴△DGO≌△BHO(AAS),
∴DG=BH;
又∵DG∥BC,
∴四边形BHDG是平行四边形,
而GB=GD,
∴四边形BGDH为菱形;
设AG=x,则BG=DG=8-x,
在直角△ABG中,由勾股定理得:
(8-x)2=x2+62
解得:x=1.75,
即AG=1.75;BG=8-1.75=6.25,
∴菱形BGDH的面积为6.25×6=37.5;
又∵菱形BGDH的面积=
BD•GH=37.5,
∴GH=7.5.
故选:D.
 解:连接BD交GH于点O;
解:连接BD交GH于点O;由题意得:GB=GD,BO=DO,BD⊥GH;
∵四边形ABCD为矩形,
∴∠C=90°,DC=AB=6,DG∥BC;
由勾股定理得:BD2=BC2+DC2=64+36=100,
∴BD=10;
∵DG∥BC,
∴∠DGO=∠BHO;
在△DGO与△BHO中,
|
∴△DGO≌△BHO(AAS),
∴DG=BH;
又∵DG∥BC,
∴四边形BHDG是平行四边形,
而GB=GD,
∴四边形BGDH为菱形;
设AG=x,则BG=DG=8-x,
在直角△ABG中,由勾股定理得:
(8-x)2=x2+62
解得:x=1.75,
即AG=1.75;BG=8-1.75=6.25,
∴菱形BGDH的面积为6.25×6=37.5;
又∵菱形BGDH的面积=
| 1 |
| 2 |
∴GH=7.5.
故选:D.
点评:该命题主要考查了翻折变换及其应用问题;同时还渗透了对菱形的判定、勾股定理、菱形的面积公式等几何知识点的考查;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
把方程x2+4x-1=0配方成(x+m)2=n的形式,则m和n的值分别是多少?( )
| A、m=2,n=3 |
| B、m=2,n=5 |
| C、m=-2,n=3 |
| D、m=-2,n=5 |
 对数轴上的点P进行如下:先把点P表示的数乘以
对数轴上的点P进行如下:先把点P表示的数乘以