题目内容
15.已知在△ABC中,AB=AC,点D、E在边BC上,将△ABD绕着点A旋转,得到△ACD′,接连D′E交AC于点O.(1)如图1,当∠BAC=120°,∠DAE=60°时,求证:DE=D′E;
(2)如图2,当∠DAE=45°,∠BAC=90°,BD=$\frac{\sqrt{2}}{2}$DE时,在不舔加任何辅助线的情况下,请直接写出图2中的所有的全等三角形.
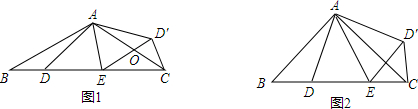
分析 (1)根据旋转的性质和全等三角形的判定定理SAS证得△DAE≌△D′AE,则由“全等三角形的对应边相等”的性质证得结论;
(2)根据旋转的性质得到△ABD≌△AD′C,∠BAD=∠DAC,∠ACD′=∠B,AD=AD′,根据等腰直角三角形的性质得到∠BAD+∠CAE=45°,推出∠DAC+∠CAE=45°,得到∠DAE=∠DAC,证得△ADE≌△AD′E,根据全等三角形的性质得到DE=D′E,由BD=$\frac{\sqrt{2}}{2}$DE,等量代换得到CD=$\frac{\sqrt{2}}{2}$DE,求得∠DEC=45°,推出△CDE是等腰直角三角形,根据线段垂直平分线的判定得到AC垂直平分DE,得到AE=AD,根据全等三角形的判定定理即可得到结论.
解答 (1)证明:∵△ABD绕点A旋转,得到△ACD′,
∴∠DAD′=∠BAC=120°,AD=AD′.
∵∠DAE=60°,
∴∠EAD′=∠DAD′-∠DAE=120°-60°=60°,
∴∠DAE=∠D′AE.
在△DAE与△D′AE中,
$\left\{\begin{array}{l}{AD=AD′}\\{∠DAE=∠D′AE}\\{AE=AE}\end{array}\right.$,
∴△DAE≌△D′AE(SAS),
∴DE=D′E(全等三角形的对应边相等);
(2)∵将△ABD绕着点A旋转,得到△ACD′,
∴△ABD≌△AD′C,∠BAD=∠DAC,∠ACD′=∠B,AD=AD′,
∵∠DAE=45°,∠BAC=90°,
∴∴∠BAD+∠CAE=45°,
∴∠DAC+∠CAE=45°,
∴∠DAE=∠DAC,
在△ADE与△AD′E中,$\left\{\begin{array}{l}{AD=AD′}\\{∠DAE=∠D′AE}\\{AE=AE}\end{array}\right.$,
∴△ADE≌△AD′E,
∴DE=D′E,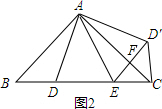
∵∠B=∠ACB=∠ACD′=45°,
∴∠D′CE=90°,
∵BD=$\frac{\sqrt{2}}{2}$DE,
∴CD=$\frac{\sqrt{2}}{2}$DE,
∴∠DEC=45°,
∴△CDE是等腰直角三角形,
∴AC垂直平分DE,
∴AE=AD,
∴△AEF≌△ADF,△CEF≌△CDF,△AEC≌△ADC,
∴△ABD≌△ACE,
∴CE=BD,
∴BE=CD,
在△ABD与△ACD中,$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠ACB}\\{BE=CD}\end{array}\right.$,
∴△ABE≌△ACD,
∴图2中的所有的全等三角形有:△ABD≌△AD′C,△ADE≌△AD′E,△AEF≌△ADF,△CEF≌△CDF,△AEC≌△ADC,△ABD≌△ACE,△ABE≌△ACD.
点评 本题考查了旋转的性质、全等三角形的判定与性质以及等腰三角形的性质,知道旋转前、后的图形全等是解题的关键.

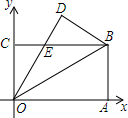 如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )
如图,长方形OABC沿OB折叠,∠AOB=30°,点B的坐标为(3,$\sqrt{3}$),OD交BC于点E,则点E的坐标为( )| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,$\sqrt{3}$) | C. | (2,$\sqrt{3}$) | D. | ($\frac{3}{2}$,$\sqrt{3}$) |
 如图,PA、PB分别与⊙O相切于A、B两点,若∠P=50°,则∠C的大小等于( )
如图,PA、PB分别与⊙O相切于A、B两点,若∠P=50°,则∠C的大小等于( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
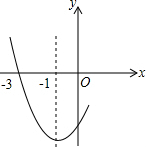 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0,④a+b+c=0.其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0,④a+b+c=0.其中说法正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ②③④ |
| A. | -1<x≤3 | B. | -1<x<3 | C. | x>-1 | D. | x≤3 |
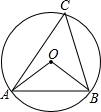 如图,锐角△ABC的顶点A,B,C都在⊙O上,∠OAB=25°,则∠C的度数为65度.
如图,锐角△ABC的顶点A,B,C都在⊙O上,∠OAB=25°,则∠C的度数为65度.