题目内容
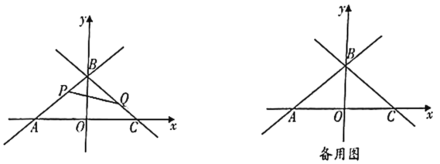
【题目】如图，在平面直角坐标系中，点
为坐标原点，直线
与
轴交于点
，与
轴交于点
，直线
与轴交于点
，且点与点关于轴对称．
（1）求直线的解析式；
（2）点
为线段
上一点，点
为线段上一点，
，连接
，设点的横坐标为
，
的面积为
（
），求与之间的函数关系式（不要求写出自变量的取值范围）；
（3）在（2）的条件下，当取最大值时，若点
是平面内的一点，在直线上是否存在点
，使得以点，，，为顶点的四边形是菱形，若存在，请直接写出符合条件的点坐标；若不存在，请说明理由．
【答案】(1) 
；(2) 
；(3)存在，N点坐标为(
，
)或(
，
)或(0，3)或(
，
)
【解析】
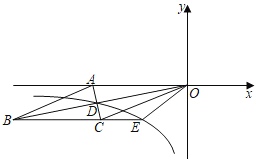
(1)求出A(-4，0)，B(0，3)，C(4，0)，利用待定系数法求BC的解析式即可；
(2)过点A作AD⊥BC于点D，过点P作PE⊥BC于点E，PF⊥OB于点F，设点P的坐标为(
，
)，求出AD的长，利用三角形函数求出
，BQ=AB-PB=5+
，再由
，代入所求量即可求解；
(3)由(2)求出P、Q点坐标，分四种情况分别求N点坐标：当N点在PQ上方时；当N点在PQ下方时；当PQ为菱形对角线时；当PN为菱形对角线时．
(1)对于直线
当
，
；当
，
，
∴
，
∵点C与点A关于y轴对称，
∴点C的坐标为
，
设直线BC的解析式为
，
将点B、C代入解析式可得：
，
解得：
，
∴直线BC的解析式为；
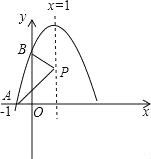
(2)如图：过点A作AD⊥BC于点D，过点P作PE⊥BC于点E，PF⊥OB于点F，
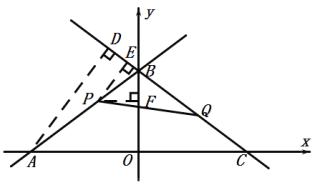
∵，C，
∴OA=OC=4，OB=3，
∴AC=8，AB=BC=
5，
∴
，即
，
∴
，
∵点P在直线
上，
设点P的坐标为(，)，
∴
，cos∠BPF=cos∠BAO，
即
，
∴
，
∵
，
∴
，
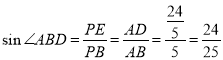∵AP=BQ，
∴
，
∴
；
(3)∵
，
∴当
时，S有最大值，
∴点P的坐标为(
，
)，
∴
，
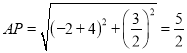∵点Q在直线上，
设点Q的坐标为(
，
)，
∵
，
∴
，
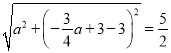解得：
，
∵Q在线段BC上，
∴
，
∴点Q的坐标为(
，)，
∴PQ∥x轴，
∴
，
如图：当N点在PQ上方时，过N点作NH⊥PQ交于点H，
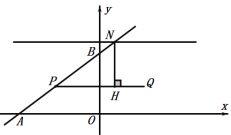
∵PQ∥
轴，
∴
，
∵PN=PQ=4，
∴
，
∴N点纵坐标为
，
∴N点横坐标为
，
解得：
，
∴点N的坐标为(，)，
同理，当N点在PQ下方时，N点纵坐标为
，
∴点N的坐标为(，)；
∵P、Q关于y轴对称，当PQ为菱形对角线时，
∴当点N的坐标为(0，3)时，NPMQ是菱形；
如图：当PN为菱形对角线时，
作Q点关于直线对称的点为M，
设QM与PN的交点为G，过G点作LK⊥PQ交PQ于点K，交MN于点L，
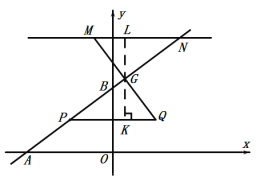
∵MQ⊥PN，
，
∴
，
∴
，
∴
，
∴
，
∵点P，Q，N，M为顶点的四边形是菱形，且PN为菱形对角线，
∴MN∥PQ，即ML∥KQ，
又∵Q点关于直线对称的点为M，
∴QG=GM
∴
，
∴
，
∴N点纵坐标为
，
∴N点横坐标为
，
解得：
，
∴点N的坐标为(，)，
综上所述：点P，Q，M，N为顶点的四边形是菱形时，N点坐标为(，)或(，)或(0，3)或(，) ．
