题目内容
在锐角三角形ABC中，若
+|tanB-
|=0，则∠C= ．
| 2cos2A-1 |
| 3 |
考点：特殊角的三角函数值,非负数的性质：绝对值,非负数的性质：算术平方根,三角形内角和定理
专题：
分析：根据非负数的性质求出cosA和tanB的值，然后求学∠A和∠B的度数，最后即可求出∠C的度数．
解答：解：∵
+|tanB-
|=0，
∴cosA=
，tanB=
，
∵△ABC为锐角三角形，
∴∠A=45°，∠B=60°，
∴∠C=180°-45°-60°=75°．
故答案为：75°．
| 2cos2A-1 |
| 3 |
∴cosA=
| ||
| 2 |
| 3 |
∵△ABC为锐角三角形，
∴∠A=45°，∠B=60°，
∴∠C=180°-45°-60°=75°．
故答案为：75°．
点评：本题考查了非负数的性质和特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．
练习册系列答案
名校课堂系列答案
相关题目
如图，直线y=| 1 |
| 2 |
| 4 |
| x |
| k |
| x |
| A、b=1，k=4 |
| B、b=2，k=12 |
| C、b=1，k=12 |
| D、b=2，k=9 |
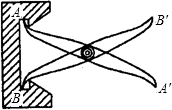如图，把两根钢条AA′，BB′的中点O连在一起，可以做成一个测量工件内槽宽的工具（工人把这种工具叫卡钳）只要量出A′B′的长度，就可以知道工件的内径AB是否符合标准，你能简要说出工人这样测量的道理吗？