题目内容
解方程组:
.
|
考点:高次方程
专题:
分析:由x2-xy-2y2=0得出(x-2y)(x+y)=0,推出x-2y=0,x+y=0,组成两个方程组,求出方程组的解即可.
解答:解:由x2-xy-2y2=0得:(x-2y)(x+y)=0,
x-2y=0,x+y=0,
即组成两个方程组:
,
,
解方程组得:
或
,
即原方程组的解为:
或
.
x-2y=0,x+y=0,
即组成两个方程组:
|
|
解方程组得:
|
|
即原方程组的解为:
|
|
点评:本题考查了解二元一次方程组和解高次方程组的应用,解此题的关键是能把高次方程组转化成二元一次方程组.

练习册系列答案
相关题目
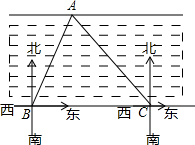 如图,某施工单位为测得某河段的宽度,测量员先在河对岸边取一点A,再在河这边沿河边取两点B、C,在点B处测得A在北偏东30°方向上,在点C处测得点A在西北方向上,量得BC长为400米,请你求出该河段的宽度.(结果保留根号)
如图,某施工单位为测得某河段的宽度,测量员先在河对岸边取一点A,再在河这边沿河边取两点B、C,在点B处测得A在北偏东30°方向上,在点C处测得点A在西北方向上,量得BC长为400米,请你求出该河段的宽度.(结果保留根号) 已知:如图,在?ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.
已知:如图,在?ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC. 如图,经测量可知等臂跷跷板AB的长为6m(OA=OB),支撑点O到地面的高度OH为0.78m,当其一端B碰到地面时,AB与地面的夹角为α.
如图,经测量可知等臂跷跷板AB的长为6m(OA=OB),支撑点O到地面的高度OH为0.78m,当其一端B碰到地面时,AB与地面的夹角为α. 如图,摩天轮⊙P的最高处A到地面l的距离是82米,最低处B到地面l的距离是2米.若游客从B处乘摩天轮绕一周需12分钟,则游客从B处乘摩天轮到地面l的距离是62米时最少需
如图,摩天轮⊙P的最高处A到地面l的距离是82米,最低处B到地面l的距离是2米.若游客从B处乘摩天轮绕一周需12分钟,则游客从B处乘摩天轮到地面l的距离是62米时最少需