题目内容
 如图,在Rt△ABC中,AC=8,BC=6,∠C=90°.⊙I分别切AC,BC,AB于点D,E,F,求Rt△ABC的内心I与外心O之间的距离.
如图,在Rt△ABC中,AC=8,BC=6,∠C=90°.⊙I分别切AC,BC,AB于点D,E,F,求Rt△ABC的内心I与外心O之间的距离.考点:三角形的内切圆与内心
专题:
分析:连结ID、IE、IF,如图,由AC=8,BC=6,∠C=90°,根据圆周角定理的推论和勾股定理得到AB为△ABC的外接圆的直径,AB=10,则外心O为AB的中点,BO=
AB=5,连结OI,设⊙I的半径为r,根据切线的性质和切线长定理得ID⊥AC,IE⊥BC,IF⊥AB,AD=AF,BE=BF,易得四边形IDCE为正方形,则DC=CE=r,所以AD=AC-DC=8-r,BE=BC-CE=6-r,即AF=8-r,BF=6-r,利用AF+BF=AB得8-r+6-r=10,解得r=2,所以BF=4,则OF=OB-BF=1,
在Rt△IOF中,根据勾股定理得IO=
.
| 1 |
| 2 |
在Rt△IOF中,根据勾股定理得IO=
| 5 |
解答: 解:连结ID、IE、IF,如图,
解:连结ID、IE、IF,如图,
∵AC=8,BC=6,∠C=90°,
∴AB为△ABC的外接圆的直径,AB=
=10,
∴外心O为AB的中点,
∴BO=
AB=5,
连结OI,如图,
设⊙I的半径为r,
∵⊙I分别切AC,BC,AB于点D,E,F,
∴ID⊥AC,IE⊥BC,IF⊥AB,AD=AF,BE=BF,
而∠C=90°,
∴四边形IDCE为正方形,
∴DC=CE=r,
∴AD=AC-DC=8-r,BE=BC-CE=6-r,
∴AF=8-r,BF=6-r,
而AF+BF=AB,
∴8-r+6-r=10,解得r=2,
∴BF=6-r=4,
∴OF=OB-BF=5-4=1,
在Rt△IOF中,IF=2,OF=1,
∴IO=
=
,
即Rt△ABC的内心I与外心O之间的距离为
.
 解:连结ID、IE、IF,如图,
解:连结ID、IE、IF,如图,∵AC=8,BC=6,∠C=90°,
∴AB为△ABC的外接圆的直径,AB=
| AC2+BC2 |
∴外心O为AB的中点,
∴BO=
| 1 |
| 2 |
连结OI,如图,
设⊙I的半径为r,
∵⊙I分别切AC,BC,AB于点D,E,F,
∴ID⊥AC,IE⊥BC,IF⊥AB,AD=AF,BE=BF,
而∠C=90°,
∴四边形IDCE为正方形,
∴DC=CE=r,
∴AD=AC-DC=8-r,BE=BC-CE=6-r,
∴AF=8-r,BF=6-r,
而AF+BF=AB,
∴8-r+6-r=10,解得r=2,
∴BF=6-r=4,
∴OF=OB-BF=5-4=1,
在Rt△IOF中,IF=2,OF=1,
∴IO=
| OF2+IF2 |
| 5 |
即Rt△ABC的内心I与外心O之间的距离为
| 5 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,.三角形的内心就是三角形三个内角角平分线的交点.也考查了切线的性质和切线长定理.

练习册系列答案
相关题目
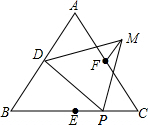 如图,D,E,F分别是正三角形ABC的边AB,BC,AC的中点,P为BC上任意一点,△DPM为正三角形.求证:PE=FM.
如图,D,E,F分别是正三角形ABC的边AB,BC,AC的中点,P为BC上任意一点,△DPM为正三角形.求证:PE=FM.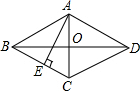 在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4cm,求菱形的面积和对角线BD的长.
在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4cm,求菱形的面积和对角线BD的长.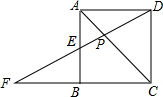 如图,正方形ABCD中,F是CB延长线上的一点,DF交AB于E,交对角线AC于P,如PE=2,EF=3.求PD的长.
如图,正方形ABCD中,F是CB延长线上的一点,DF交AB于E,交对角线AC于P,如PE=2,EF=3.求PD的长. 如图,圆周角∠ACB的度数为34°,∠OAC=60°,则圆心角∠AOB的度数为
如图,圆周角∠ACB的度数为34°,∠OAC=60°,则圆心角∠AOB的度数为