题目内容
7. 如图.把直角三角形ABC的斜边AB放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C′的位置上,已知BC=1,∠A=30°.则顶点A运动到A″的位置时,点A经过的路线有多长?点A经过的路线与直线l所围成的面积有多大?
如图.把直角三角形ABC的斜边AB放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C′的位置上,已知BC=1,∠A=30°.则顶点A运动到A″的位置时,点A经过的路线有多长?点A经过的路线与直线l所围成的面积有多大?
分析 (1)点A经过的路线长是两段弧长,利用弧长公式计算.
(2)点A经过的路线与直线l所围成的面积是两个扇形的面积加上一个直角三角形的面积,按扇形面积公式和三角形面积公式计算.
解答 解:(1)Rt△ABC中,BC=1,∠A=30°,
则可得AB=2,AC=$\sqrt{3}$,∠CBA=60°,∠ABA′=120°,
则点A到A″所经过的路线为:,l弧AA′+l弧A′A″=$\frac{120π×2}{180}$+$\frac{90π×\sqrt{3}}{180}$=$\frac{4π}{3}$+$\frac{\sqrt{3}}{2}π$.
(2)点A经过的路线与直线l围成的面积为:$\frac{120π•{2}^{2}}{360}$+$\frac{90π•(\sqrt{3})^{2}}{360}$+$\frac{1}{2}×1×\sqrt{3}$=$\frac{25π}{12}$+$\frac{\sqrt{3}}{2}$.
点评 本题考查弧长公式、扇形面积公式,在做这道题时,分清这两个弧长,扇形的圆心角和半径分别是多少是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图1,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为直线x=2,与x轴的一个交点是(-1,0);
如图1,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为直线x=2,与x轴的一个交点是(-1,0); 如图,点C在线段BE上,在BE的同侧作△ABC和△DCE,AE,BD交于点P,已知AC=BC,DC=EC,∠1=∠2.
如图,点C在线段BE上,在BE的同侧作△ABC和△DCE,AE,BD交于点P,已知AC=BC,DC=EC,∠1=∠2.
 如图,边长为$\sqrt{3}$的等边△ABC中,D、E分别为AB、BC上的点,且DB=$\sqrt{2}$,将线段ED绕E点顺时针旋转60°得到线段EF,连CF.当∠FCB=30°时,CE的长为$\frac{1}{2}$($\sqrt{3}$+$\sqrt{2}$).
如图,边长为$\sqrt{3}$的等边△ABC中,D、E分别为AB、BC上的点,且DB=$\sqrt{2}$,将线段ED绕E点顺时针旋转60°得到线段EF,连CF.当∠FCB=30°时,CE的长为$\frac{1}{2}$($\sqrt{3}$+$\sqrt{2}$).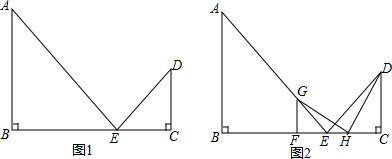
 已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a-b+c<0;⑤3a+c>0;则正确的结论是
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a-b+c<0;⑤3a+c>0;则正确的结论是