题目内容
19.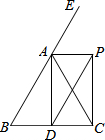 如图,△ABC中,AB=AC,D是BC边的中点,E是BA延长线上一点,AP平分∠EAC,DP∥AB交AP于点P,求证:四边形ADCP是矩形.
如图,△ABC中,AB=AC,D是BC边的中点,E是BA延长线上一点,AP平分∠EAC,DP∥AB交AP于点P,求证:四边形ADCP是矩形.
分析 根据DP∥AB,AP∥BC,得出四边形ABDP是平行四边形,AP=BD,再根据BD=CD,得出AP=CD,四边形APCD是平行四边形,最后根据∠ADC=90°,即可证出四边形APCD是矩形;
解答 解:∵AB=AC,∠BAD=∠CAD,
∴AD⊥BC,
∴∠ADB=90°,
∵AP平分∠FAC,
∴∠PAD=∠ADB=90°,
∴AP∥BC;
∵DP∥AB,
∴四边形ABDP是平行四边形,
∴AP=BD,
∵BD=CD,
∴AP=CD,
∴四边形APCD是平行四边形,
∵∠ADC=90°,
∴四边形ADCP是矩形;
点评 此题考查了矩形的判定和性质的综合应用,用到的知识点是平行四边形的判断与性质、等腰三角形的性质、平行线的性质,关键是综合利用有关性质,得出结论,是中考命题的热点.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
10.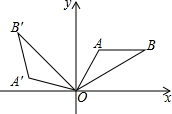 如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
 如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )| A. | (-2,2$\sqrt{2}$) | B. | (-2$\sqrt{2}$,2) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
4.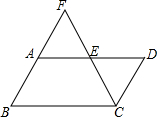 如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )
如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )
 如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )
如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )| A. | △AEF≌△CED | B. | CF=AD | C. | AF=CD | D. | BF=CF |
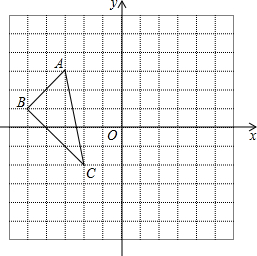 按要求画出图形:
按要求画出图形:
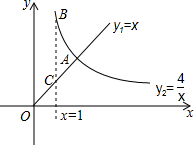 如图,直线和双曲线分别是函数y1=x(x≥0),y2=$\frac{4}{x}$(x>0)的图象,则以下结论:
如图,直线和双曲线分别是函数y1=x(x≥0),y2=$\frac{4}{x}$(x>0)的图象,则以下结论: