题目内容
为了抓住中秋商机,某超市决定购进A,B两种月饼,若购进A种月饼10盒,B种月饼5盒,需要600元;若购进A种月饼5盒,B种月饼3盒,需要330元.
(1)求购进A,B两种月饼每盒多少元.
(2)该超市决定拿出6000元全部用来购进两种月饼,考虑市场需求,要求购进A种月饼的数量不少于B种月饼数量6倍,且不超过B种月饼数量的8倍,那么该超市共有几种进货方案?
(3)若销售每盒A种月饼可获利20元,销售每盒B种月饼可获利30元,在(2)题的各种进货方案,哪一种获利最大?最大利润是多少元?
(1)求购进A,B两种月饼每盒多少元.
(2)该超市决定拿出6000元全部用来购进两种月饼,考虑市场需求,要求购进A种月饼的数量不少于B种月饼数量6倍,且不超过B种月饼数量的8倍,那么该超市共有几种进货方案?
(3)若销售每盒A种月饼可获利20元,销售每盒B种月饼可获利30元,在(2)题的各种进货方案,哪一种获利最大?最大利润是多少元?
考点:一元一次不等式组的应用,二元一次方程组的应用
专题:
分析:(1)关系式为:A的单价×数量+B的单价×数量=总费用;
(2)关系式为:A需要的钱数+B需要的钱数=6000;购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍;
(3)计算出各种方案的利润,比较即可.
(2)关系式为:A需要的钱数+B需要的钱数=6000;购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍;
(3)计算出各种方案的利润,比较即可.
解答:解:(1)购进A,B两种月饼每盒分别是x元,y元.
,
解得:
.
答:购进A,B两种月饼每盒分别是30元,60元;
(2)设购买A种月饼为a盒,B种月饼为b盒.则
,
解得 20≤b≤25.
则b=20,21,22,23,24,25;
则a对应为 160,158;154;152,150,148.
答:商店共有6种进货方案:
方案一:购买A种月饼160盒,B种月饼20盒;
方案二:购买A种月饼158盒,B种月饼21盒;
方案三:购买A种月饼154盒,B种月饼22盒;
方案四:购买A种月饼152盒,B种月饼23盒;
方案五:购买A种月饼150盒,B种月饼24盒;
方案六:购买A种月饼148盒,B种月饼25盒;
(3)设利润为W元,则W=20a+30b,
∵30a+60b=6000,
∴a=200-2b,
∴代入上式得:W=-10b+4000,
∵-10<0,
∴W随着b的增大而减小,
∴当b=20时,W最大,即此时a=160时,W最大,
∴W最大=-10×20+4000=3800(元),
答:方案获利最大为:A种月饼160盒,B种月饼20盒,最大利润为3800元.
|
解得:
|
答:购进A,B两种月饼每盒分别是30元,60元;
(2)设购买A种月饼为a盒,B种月饼为b盒.则
|
解得 20≤b≤25.
则b=20,21,22,23,24,25;
则a对应为 160,158;154;152,150,148.
答:商店共有6种进货方案:
方案一:购买A种月饼160盒,B种月饼20盒;
方案二:购买A种月饼158盒,B种月饼21盒;
方案三:购买A种月饼154盒,B种月饼22盒;
方案四:购买A种月饼152盒,B种月饼23盒;
方案五:购买A种月饼150盒,B种月饼24盒;
方案六:购买A种月饼148盒,B种月饼25盒;
(3)设利润为W元,则W=20a+30b,
∵30a+60b=6000,
∴a=200-2b,
∴代入上式得:W=-10b+4000,
∵-10<0,
∴W随着b的增大而减小,
∴当b=20时,W最大,即此时a=160时,W最大,
∴W最大=-10×20+4000=3800(元),
答:方案获利最大为:A种月饼160盒,B种月饼20盒,最大利润为3800元.
点评:本题考查了一元一次不等式组、二元一次不等式组的应用.解决本题的关键是读懂题意,找到符合题意的相应的关系式是解决问题的关键,注意第二问应求得整数解.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 如图,D、E分别在BC、AC边上,且∠B=∠C,AD=DE,∠ADB=∠DEC.
如图,D、E分别在BC、AC边上,且∠B=∠C,AD=DE,∠ADB=∠DEC.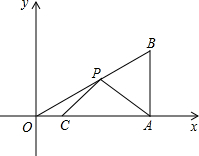 如图,在平面直角坐标系xOy中,Rt△OAB的顶点A的坐标为(9,0),∠AOB=30°,点C的坐标为(2,0),点P为斜边OB上的一个动点,则PA+PC的最小值为
如图,在平面直角坐标系xOy中,Rt△OAB的顶点A的坐标为(9,0),∠AOB=30°,点C的坐标为(2,0),点P为斜边OB上的一个动点,则PA+PC的最小值为