题目内容
已知平行四边形ABCD，点E是CD的中点，连结BE并延长与AD的延长线交于F，且与对角线AC交于M．求证：BM•EF=BF•EM．考点：相似三角形的判定与性质,平行四边形的性质
专题：证明题
分析：根据平行四边形的性质得出DC=AB，AD∥BC，CD∥AB，根据相似三角形的判定得出△AMB∽△CME，△BEC∽△FED，得出比例式，变形后得出即可．
解答：证明：∵点E是CD的中点，
∴DE=CE，
∵四边形ABCD是平行四边形，
∴DC=AB，AD∥BC，CD∥AB，
∴△AMB∽△CME，△BEC∽△FED，
∴
=
，
=
，
∴
=
，
∵CD=AB，DE=CE，
∴
=
，
∴BM•EF=BF•EM．
∴DE=CE，
∵四边形ABCD是平行四边形，
∴DC=AB，AD∥BC，CD∥AB，
∴△AMB∽△CME，△BEC∽△FED，∴
| BM |
| EM |
| AB |
| CE |
| BE |
| EF |
| CE |
| DE |
∴
| BF |
| EF |
| CD |
| DE |
∵CD=AB，DE=CE，
∴
| BM |
| EM |
| BF |
| EF |
∴BM•EF=BF•EM．
点评：本题考查了相似三角形的性质和判定，平行四边形的性质的应用，主要考查学生的推理能力．
练习册系列答案
相关题目
当a是偶数时，（x-y）a•（y-x）b与（y-x）a+b的关系是（ ）
| A、相等 | B、互为倒数 |
| C、互为相反数 | D、无法确定 |
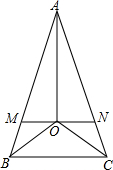如图，在△ABC中，AB=AC，∠B与∠C的角平分线交于点O，过点O作MN∥BC，分别交AB，AC于M，N，连接AO．