题目内容
2.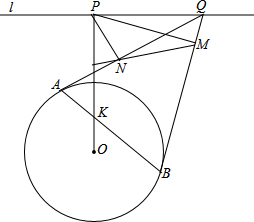 如图,圆O(圆心为O)与直线l相离,作OP⊥l,P为垂足.设点Q是l上任意一点(不与点P重合),过点Q作圆O的两条切线QA和QB,A和B为切点,AB与OP相交于点K.过点P作PM⊥QB,PN⊥QA,M和N为垂足.求证:直线MN平分线段KP.
如图,圆O(圆心为O)与直线l相离,作OP⊥l,P为垂足.设点Q是l上任意一点(不与点P重合),过点Q作圆O的两条切线QA和QB,A和B为切点,AB与OP相交于点K.过点P作PM⊥QB,PN⊥QA,M和N为垂足.求证:直线MN平分线段KP.
分析 连接AO,BO,作PI⊥AB于I,记J为直线MN与线段PK的交点,根据切线的性质得到∠QAO=∠QBO=∠QPO=90°,推出O、B、Q、P、A均在以线段OQ为直径的圆周上,由西姆松定理知△QAB的外接圆上一点P在其三边的垂足N、M、I三点共线,即N、M、J、I四点共线,根据平行线的性质得到∠POQ=∠IPO,根据圆周角定理得到∠PLJ=∠PIM=∠PAM=∠POQ,即可得到结论.
解答 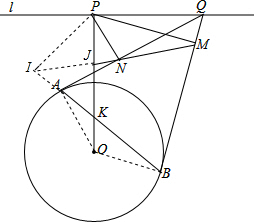 连接AO,BO,作PI⊥AB于I,记J为直线MN与线段PK的交点,
连接AO,BO,作PI⊥AB于I,记J为直线MN与线段PK的交点,
∵QA,QB是⊙O的两条切线,
∴∠QAO=∠QBO=∠QPO=90°,
故O、B、Q、P、A均在以线段OQ为直径的圆周上,
∵PM⊥QB,PN⊥QA,
由西姆松定理知:△QAB的外接圆上一点P在其三边的垂足N、M、I三点共线,
即N、M、J、I四点共线,
∵QO⊥AB,PI⊥AB,
∴QO∥PI,
∴∠POQ=∠IPO,
∵P、A、I、N四点共圆,P、A、O、Q也四点共圆,
∴∠PLJ=∠PIM=∠PAM=∠POQ,
在直角三角形PIK中,∠PLJ=∠JPI,
∴J为PK的中点,
∴直线MN平分线段KP.
点评 本题考查了四点共圆,线段垂直平分线的判定,等腰三角形的性质,切线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
4.如果多项式x2-5x+m分解因式的结果为(x-3)(x+n),那么m,n的值分别为( )
| A. | m=-2,n=6 | B. | m=2,n=-6 | C. | m=6,n=-2 | D. | m=-6,n=-2 |
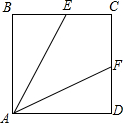 如图,点E、F位于正方形ABCD边BC、CD上.
如图,点E、F位于正方形ABCD边BC、CD上.