题目内容
9.如图所示,A,B是坐标轴正半轴上的两点,过点B作PB⊥y轴交双曲线y=$\frac{6}{x}$(x>0)于P点,A,B两点的坐标分别为(1,0),(0,3),x轴上的动点M在点A的右侧,动点N在射线BP上,过点A作AB的垂线,交射线BP于D点,交直线MN于Q点,连结BQ,取BQ的中点C,若以A,C,N,Q为顶点的四边形是平行四边形,则Q点的坐标为(4,1)或(28,9).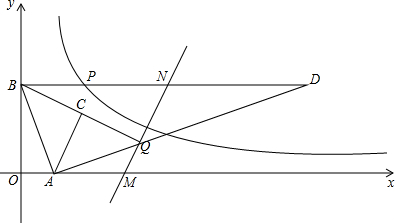
分析 首先求出直线AD的解析式,求出点D坐标,分两种情形讨论①如图1中,当Q在线段AD上时,作QE⊥x轴于E,DF⊥x轴于F.②如图2中,当点Q在AD的延长线上时,作QF⊥x轴于F,DE⊥AF于E.分别求解即可.
解答 解:∵A(1,0),B(0,3),
∴直线AB的解析式为y=-3x+3,
∵AD⊥AB,
∴直线AD的解析式为y=$\frac{1}{3}$x-$\frac{1}{3}$,
∵BD⊥y轴,
∴BD∥OA,
∴D(10,3),
①如图1中,当Q在线段AD上时,作QE⊥x轴于E,DF⊥x轴于F.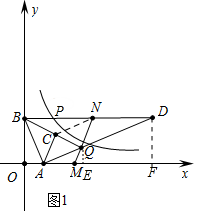
∵四边形ACNQ是平行四边形,
∴AQ=CN,CN∥AD,
∵BC=CQ,
∴BN=ND,
∴DQ=2CN=2AQ,
∵QE∥DF,
∴$\frac{AQ}{AD}$=$\frac{QE}{DF}$=$\frac{AE}{AF}$=$\frac{1}{3}$,
∵AF=9,DF=3,
∴QE=1,AE=3,
∴点Q坐标为(4,1).
②如图2中,当点Q在AD的延长线上时,作QF⊥x轴于F,DE⊥AF于E.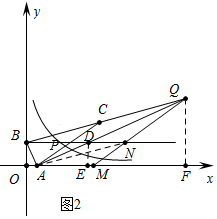
∵四边形ACQN是平行四边形,
∴AN∥BQ,AN=CQ,
∴$\frac{AN}{BQ}$=$\frac{AD}{DQ}$,∵BC=CQ,
∴$\frac{AD}{DQ}$=$\frac{1}{2}$,
∵DE∥QF,
∴$\frac{DE}{QF}$=$\frac{AE}{AF}$=$\frac{AD}{AQ}$=$\frac{1}{3}$,
∵AE=9,DE=3,
∴QF=9,AF=27,
∴点Q坐标(28,9),
综上所述点Q坐标(4,1)或(28,9).
故答案为(4,1)或(28,9).
点评 本题考查反比例函数,相似三角形的判定和性质、平行线等分线段定理、一次函数等知识,解题的关键是灵活运用相似三角形的性质解决问题,学会分类讨论的思想思考问题,属于中考填空题中的压轴题.

 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案| A. | m=-2,n=6 | B. | m=2,n=-6 | C. | m=6,n=-2 | D. | m=-6,n=-2 |
| A. | 9x+2 | B. | 9x-2 | C. | -$\frac{2}{9}$x | D. | $\frac{2}{9}$x |
 如图,已知抛物线y=ax2+bx-3与直线y=x交于A,B两点,且A,B两点的横坐标分别为-1和3.
如图,已知抛物线y=ax2+bx-3与直线y=x交于A,B两点,且A,B两点的横坐标分别为-1和3. 小明想把一长为25cm,宽为20cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.
小明想把一长为25cm,宽为20cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.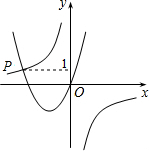 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解为( )
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解为( )