题目内容
1.计算:($\frac{1}{2}$)-1-(2017-π)0-2sin45°+|$\sqrt{2}$-1|分析 分别计算:①($\frac{1}{2}$)-1=21=2,
②(2017-π)0=1,
③sin45°=$\frac{\sqrt{2}}{2}$,
④∵$\sqrt{2}$>1,
∴|$\sqrt{2}$-1|=$\sqrt{2}$-1.
最后代入按有理数的混合运算法则进行计算即可.
解答 解:原式=2-1-2×$\frac{\sqrt{2}}{2}$+$\sqrt{2}$-1,
=2-1-$\sqrt{2}$+$\sqrt{2}$-1,
=0.
点评 本题考查实数的综合运算能力,解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、绝对值的运算,是常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中a的值5%;
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?
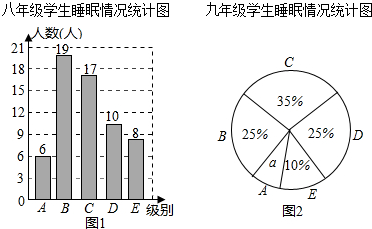
睡眠情况分段情况如下
| 组别 | 睡眠时间x(小时) |
| A | 4.5≤x<5.5 |
| B | 5.5≤x<6.5 |
| C | 6.5≤x<7.5 |
| D | 7.5≤x<8.5 |
| E | 8.5≤x<9.5 |
(Ⅰ)直接写出统计图中a的值5%;
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?

9.在四张完全相同的卡片上,分别画有圆、菱形、等腰三角形正六边形,现从中随机抽取一张,卡片上的图形是中心对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
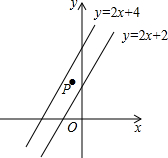 如图,在平面直角坐标系中,点P(-$\frac{1}{2}$,a)在直线y=2x+2与直线y=2x+4之间,则a的取值范围是1<a<3.
如图,在平面直角坐标系中,点P(-$\frac{1}{2}$,a)在直线y=2x+2与直线y=2x+4之间,则a的取值范围是1<a<3. 如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6$\sqrt{2}$米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6$\sqrt{2}$米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.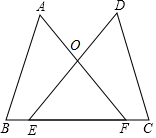 已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.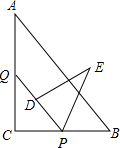 如图,在Rt△ABC中,∠C=90°,AB=15,BC=9.点P、Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,在Rt△ABC中,∠C=90°,AB=15,BC=9.点P、Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上. 如图,从电线杆离地面9m处向地面拉一条长15m的固定缆绳,这条缆绳在地面的固定点距离电线杆底部有12m.
如图,从电线杆离地面9m处向地面拉一条长15m的固定缆绳,这条缆绳在地面的固定点距离电线杆底部有12m.