题目内容
18.先化简,再求值:($\frac{2x}{x-y}$+$\frac{x}{y-x}$)÷$\frac{x}{{x}^{2}-{y}^{2}}$,其中x=2017,y=1.分析 根据分式的加法和除法可以化简题目中的式子,然后将x、y的值代入即可解答本题.
解答 解:($\frac{2x}{x-y}$+$\frac{x}{y-x}$)÷$\frac{x}{{x}^{2}-{y}^{2}}$
=$\frac{2x-x}{x-y}•\frac{(x+y)(x-y)}{x}$
=$\frac{x}{x-y}•\frac{(x+y)(x-y)}{x}$
=x+y,
当x=2017,y=1时,原式=2017+1=2018.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.在四张完全相同的卡片上,分别画有圆、菱形、等腰三角形正六边形,现从中随机抽取一张,卡片上的图形是中心对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
 如图,在边长为1的小正反形组成的网格中,△ABC的三个顶点均在格点上,则tanB的值为$\frac{3}{4}$.
如图,在边长为1的小正反形组成的网格中,△ABC的三个顶点均在格点上,则tanB的值为$\frac{3}{4}$.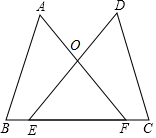 已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.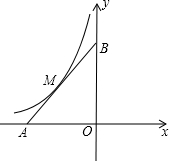 已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=-$\frac{9}{x}$的图象与线段AB交于M点,且AM=BM.
已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=-$\frac{9}{x}$的图象与线段AB交于M点,且AM=BM.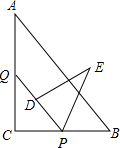 如图,在Rt△ABC中,∠C=90°,AB=15,BC=9.点P、Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,在Rt△ABC中,∠C=90°,AB=15,BC=9.点P、Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.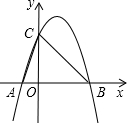 如图,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
如图,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.