题目内容
5. 将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.
将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.
分析 由题意可知:第n行有n个数,每n行的第一个数的绝对值的分母为$\frac{1}{2}$n(n+1)+1;且奇数为正,偶数为负,分子都是1;由此规律代入数值求出答案即可.
解答 解:∵第n行的第n个数的绝对值的分母为$\frac{1}{2}$n(n+1)+n,
∴第200行第100个数的分母为$\frac{1}{2}$×200×(200+1)+100=20200,
又∵奇数为正,偶数为负,分子都是1,
∴第200行第100个数为$\frac{1}{20200}$.
故答案为:$\frac{1}{20200}$.
点评 本题考查数字的排列规律,分析数据,总结、归纳数据发现规律,利用规律解决问题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
20.下列方程中,不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}x+2y=0\\ 2x+y=1\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=0}\\{y-x+5=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}x-2y-1=0\\-x=y+2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=4\\ 2x=z-2y\end{array}\right.$ |
 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点. 如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为8cm2或2$\sqrt{15}$cm2或2$\sqrt{7}$cm2.
如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为8cm2或2$\sqrt{15}$cm2或2$\sqrt{7}$cm2.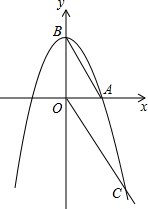 如图,抛物线y1=-x2+a与x轴正半轴交于点A,与y轴交于点B,点C(2,-3)在抛物线y1的图象上,连接AB,OC.
如图,抛物线y1=-x2+a与x轴正半轴交于点A,与y轴交于点B,点C(2,-3)在抛物线y1的图象上,连接AB,OC.