题目内容
16.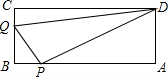 如图.A、B、C、D为矩形的4个顶点:AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止:点Q以2cm/s的速度向点B移动,经过多长时间P、Q两点之间的距离是10cm?
如图.A、B、C、D为矩形的4个顶点:AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止:点Q以2cm/s的速度向点B移动,经过多长时间P、Q两点之间的距离是10cm?
分析 设P,Q两点从出发经过t秒时,点P,Q间的距离是10cm,表示出PB、BQ,利用勾股定理建立方程求得答案即可.
解答 解:设P,Q两点从出发经过t秒时,点P,Q间的距离是10cm,
则PB=16-3t,BQ=6-2t,
∵PB2+BQ2=PQ2,
∴(16-3t)2+(6-2t)2=102,
解得t1=$\frac{60+4\sqrt{69}}{13}$,t2=$\frac{60-4\sqrt{69}}{13}$.
∵0<t<3,
∴t1=$\frac{60+4\sqrt{69}}{13}$(不合题意,舍去).
答:P,Q两点从出发经过$\frac{60-4\sqrt{69}}{13}$秒时,点P,Q间的距离是10cm.
点评 考查一元二次方程的应用;利用勾股定理得到等量关系是解决本题的关键.

练习册系列答案
相关题目
7.不能用一副三角板拼出的角是( )
| A. | 150° | B. | 105° | C. | 15° | D. | 110° |
4.xmym+n与2x3y是同类项,那么n等于( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
1.已知D、E分别是△ABC的边AB和AC的中点,F、G分别是AD、AE的中点,若△ABC的面积为16cm2,则四边形DEGF的面积为( )
| A. | 5cm2 | B. | 4cm2 | C. | 3cm2 | D. | 2cm2 |
 如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为35°.
如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为35°.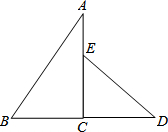 如图,是一副三角板组成的图形.
如图,是一副三角板组成的图形.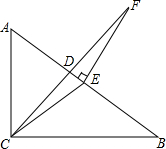 如图,在△ABC中,∠ACB=90°,CD是角平分线,点E在AB上,∠ECB=∠B,EF⊥AB交CD的延长线于点F,求证:∠F=∠DCE.
如图,在△ABC中,∠ACB=90°,CD是角平分线,点E在AB上,∠ECB=∠B,EF⊥AB交CD的延长线于点F,求证:∠F=∠DCE.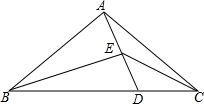 己知E为△ABC内部一点,AE延长线交边BC于点D,连按BE、CE,∠BED=∠BAC=2∠DEC.
己知E为△ABC内部一点,AE延长线交边BC于点D,连按BE、CE,∠BED=∠BAC=2∠DEC.