题目内容
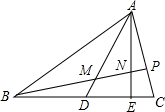 如图,△ABC中,D、E是BC边上的点,且BD:DE:EC=3:2:1,P是AC边上的点,且AP:PC=2:1,BP分别交AD、AE于M、N,则BM:MN:NP等于( )
如图,△ABC中,D、E是BC边上的点,且BD:DE:EC=3:2:1,P是AC边上的点,且AP:PC=2:1,BP分别交AD、AE于M、N,则BM:MN:NP等于( )| A、3:2:1 |
| B、5:3:1 |
| C、25:12:5 |
| D、51:24:10 |
考点:平行线分线段成比例
专题:
分析:作PF∥BC交AE于点F,作DG∥AC交BP于点G,设EC=a,则BD=3a,DE=2a.同理,设PC=b,则AP=2b.利用平行线分线段成比例定理以及比例的性质,即可利用BP分别表示出BM、MN、NP的长度,从而求解.
解答: 解:作PF∥BC交AE于点F,作DG∥AC交BP于点G.
解:作PF∥BC交AE于点F,作DG∥AC交BP于点G.
∵BD:DE:EC=3:2:1,
∴设EC=a,则BD=3a,DE=2a.
同理,设PC=b,则AP=2b.
∵NP∥BC,
∴
=
=
=
,
=
,
∴PF=
a,则
=
=
,
∴
=
,即NP=
BP,
∵DG∥AC,BD=DC=3a,
∴BG=
BP,DG=
PC=
b.
∵DG∥AC,
∴
=
=
=
,
∴
=
,
∴GM=
GP=
BP,
∴MN=BP-BG-GM-NP=BP-
BP-
BP-
BP=
BP,BM=BG+DM=
BP+
BP=
BP.
∴BM:MN:NP=
:
:
=51:24:10.
故选D.
 解:作PF∥BC交AE于点F,作DG∥AC交BP于点G.
解:作PF∥BC交AE于点F,作DG∥AC交BP于点G.∵BD:DE:EC=3:2:1,
∴设EC=a,则BD=3a,DE=2a.
同理,设PC=b,则AP=2b.
∵NP∥BC,
∴
| PF |
| EC |
| AP |
| AC |
| 2b |
| 3b |
| 2 |
| 3 |
| NP |
| NB |
| PF |
| BE |
∴PF=
| 2 |
| 3 |
| NP |
| NB |
| ||
| 5a |
| 2 |
| 15 |
∴
| NP |
| BP |
| 2 |
| 17 |
| 2 |
| 17 |
∵DG∥AC,BD=DC=3a,
∴BG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵DG∥AC,
∴
| GM |
| MP |
| DG |
| AP |
| ||
| 2b |
| 1 |
| 4 |
∴
| GM |
| GP |
| 1 |
| 5 |
∴GM=
| 1 |
| 5 |
| 1 |
| 10 |
∴MN=BP-BG-GM-NP=BP-
| 1 |
| 2 |
| 1 |
| 10 |
| 2 |
| 17 |
| 24 |
| 85 |
| 1 |
| 2 |
| 1 |
| 10 |
| 3 |
| 5 |
∴BM:MN:NP=
| 3 |
| 5 |
| 24 |
| 85 |
| 2 |
| 17 |
故选D.
点评:本题考查了平行线分线段成比例定理以及比例的性质,正确作出辅助线是关键.

练习册系列答案
相关题目
一件衣服以220元出售,可获利10%,则这件衣服的进价是( )
| A、110元 | B、180元 |
| C、198元 | D、200元 |
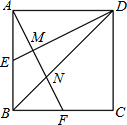 如图,正方形ABCD的边长为2
如图,正方形ABCD的边长为2| 15 |
| A、8 | ||
| B、12 | ||
C、
| ||
| D、15 |
 已知梯形ABCD中,AD∥EF∥GH∥BC,AE:EG:GB=1:2:3,AD=3,BC=9,则EF+GH=( )
已知梯形ABCD中,AD∥EF∥GH∥BC,AE:EG:GB=1:2:3,AD=3,BC=9,则EF+GH=( ) 如图,△ACB中∠ACB=90°,∠A=40°.将△ACB绕点C顺时针旋转得到△DCE,边DE恰好经过点B,则∠DCB的度数为
如图,△ACB中∠ACB=90°,∠A=40°.将△ACB绕点C顺时针旋转得到△DCE,边DE恰好经过点B,则∠DCB的度数为