题目内容
抛物线y=ax2+bx+c的图象与x轴有两个交点M(x1,0),N(x2,0),且经过点A(0,1),其中0<x1<x2.过点A的直线l与x轴交于点C,与抛物线交于点B(异于点A),满足△CAN是等腰直角三角形,且S△BMN=
S△AMN.求该抛物线的解析式 .
| 5 |
| 2 |
考点:二次函数综合题
专题:
分析:由点A(0,1)及△CAN是等腰直角三角形,可知C(-1,0),N(1,0),由A、C两点坐标可求直线AB,由S△BMN=
S△AMN,可知B点纵坐标为
,代入直线AB解析式可求B点横坐标,将A、B、N三点坐标代入y=ax2+bx+c中,可求抛物线解析式.
| 5 |
| 2 |
| 5 |
| 2 |
解答: 解:如图,由抛物线经过A(0,1),M(x1,0),N(x2,0),
解:如图,由抛物线经过A(0,1),M(x1,0),N(x2,0),
其中0<x1<x2,
可知抛物线开口向上,与x轴两交点在正半轴,
∵点A(0,1),△CAN是等腰直角三角形,∴C(-1,0),N(1,0),
设直线AB解析式为y=mx+n,
将A、C两点坐标代入,得
,解得
,
直线AB解析式为y=x+1,
∵S△BMN=
S△AMN,两三角形同底MN,△AMN的高为1,
∴△BMN的高为
,即B点纵坐标为
,把y=
代入y=x+1中,得x=
,
即B(
,
),
把A、B、N三点坐标代入y=ax2+bx+c中,得
,
解得
,
所以,抛物线解析式为y=4x2-5x+1,
故答案为:y=4x2-5x+1.
 解:如图,由抛物线经过A(0,1),M(x1,0),N(x2,0),
解:如图,由抛物线经过A(0,1),M(x1,0),N(x2,0),其中0<x1<x2,
可知抛物线开口向上,与x轴两交点在正半轴,
∵点A(0,1),△CAN是等腰直角三角形,∴C(-1,0),N(1,0),
设直线AB解析式为y=mx+n,
将A、C两点坐标代入,得
|
|
直线AB解析式为y=x+1,
∵S△BMN=
| 5 |
| 2 |
∴△BMN的高为
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
即B(
| 3 |
| 2 |
| 5 |
| 2 |
把A、B、N三点坐标代入y=ax2+bx+c中,得
|
解得
|
所以,抛物线解析式为y=4x2-5x+1,
故答案为:y=4x2-5x+1.
点评:本题考查了二次函数的综合运用.关键是根据已知条件判断抛物线开口方向及大致位置,根据特殊三角形求直线解析式,根据面积法求B点坐标,运用待定系数法求抛物线解析式.

练习册系列答案
相关题目
将正偶数按下表排成5列
根据上面排列的规律,2012应排在( )
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 2 | 4 | 6 | 8 | |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 | 18 | 20 | 22 | 24 | |
| 第4行 | 32 | 30 | 28 | 26 | |
| … | … |
| A、第502行第1列 |
| B、第250行第5列 |
| C、第251行第4列 |
| D、第252行第3列 |
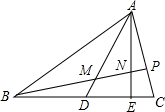 如图,△ABC中,D、E是BC边上的点,且BD:DE:EC=3:2:1,P是AC边上的点,且AP:PC=2:1,BP分别交AD、AE于M、N,则BM:MN:NP等于( )
如图,△ABC中,D、E是BC边上的点,且BD:DE:EC=3:2:1,P是AC边上的点,且AP:PC=2:1,BP分别交AD、AE于M、N,则BM:MN:NP等于( )| A、3:2:1 |
| B、5:3:1 |
| C、25:12:5 |
| D、51:24:10 |
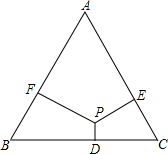 如图,△ABC是边长为12的等边三角形,点P是三角形内的一点,过P分别作边BC,CA,AB的垂线,垂足分别为D,E,F.已知PD:PE:PF=1:2:3,那么四边形BDPF的面积是
如图,△ABC是边长为12的等边三角形,点P是三角形内的一点,过P分别作边BC,CA,AB的垂线,垂足分别为D,E,F.已知PD:PE:PF=1:2:3,那么四边形BDPF的面积是