题目内容
有很多种方法可以将2001写成25个自然数之和,对于每一种写法,这25个自然数均有相应的最大公约数,那么这个最大公约数的最大值是多少?
考点:约数与倍数
专题:
分析:根据2001=3×23×29=69×(1×24+5),即2001可写成:24个69、1个69×5=345的和,或23个69、1个69×2=138,1个69×4=276的和,或23个69、2个69×3=207的和,或22个69、2个69×2=138,1个69×3=207的和,或21个69、4个69×2=138的和,这25个自然数的最大公因数必定能整除3×23×29.这些公因数中的最大值不可能超过3×29=87,否则这25个之和必定大于2001,所以最大值是3×23=69,它们的最大公因数都是69.
解答:解:因为2001=3×23×29=69×(1×24+5),
从 69×(1×24+5)可以看题目需要分多少份(本题是25份),
可以是:24个69、1个69×5=345的和,或23个69、1个69×2=138,1个69×4=276的和,
或23个69、2个69×3=207的和,或22个69、2个69×2=138,1个69×3=207的和,或21个69、4个69×2=138的和,
不管是那种情况,25个数中要么是69,要么是69的倍数,
所以他们的最大公因数都是69.
答:这个最大公因数的最大值是69.
从 69×(1×24+5)可以看题目需要分多少份(本题是25份),
可以是:24个69、1个69×5=345的和,或23个69、1个69×2=138,1个69×4=276的和,
或23个69、2个69×3=207的和,或22个69、2个69×2=138,1个69×3=207的和,或21个69、4个69×2=138的和,
不管是那种情况,25个数中要么是69,要么是69的倍数,
所以他们的最大公因数都是69.
答:这个最大公因数的最大值是69.
点评:此题主要考查公因数和公倍数问题,注意根据分解质因数情况确定多个数的最大公因数情况.

练习册系列答案
相关题目
将正偶数按下表排成5列
根据上面排列的规律,2012应排在( )
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 2 | 4 | 6 | 8 | |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 | 18 | 20 | 22 | 24 | |
| 第4行 | 32 | 30 | 28 | 26 | |
| … | … |
| A、第502行第1列 |
| B、第250行第5列 |
| C、第251行第4列 |
| D、第252行第3列 |
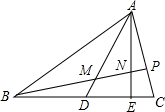 如图,△ABC中,D、E是BC边上的点,且BD:DE:EC=3:2:1,P是AC边上的点,且AP:PC=2:1,BP分别交AD、AE于M、N,则BM:MN:NP等于( )
如图,△ABC中,D、E是BC边上的点,且BD:DE:EC=3:2:1,P是AC边上的点,且AP:PC=2:1,BP分别交AD、AE于M、N,则BM:MN:NP等于( )| A、3:2:1 |
| B、5:3:1 |
| C、25:12:5 |
| D、51:24:10 |
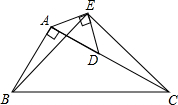 如图,在直角三角形ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板ADE如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
如图,在直角三角形ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板ADE如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.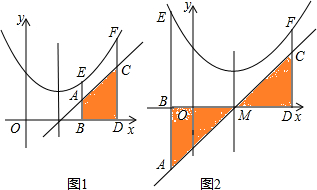 已知点E(x1,y1)、F(x2,y2)为抛物线y=ax2+bx+c上的两点,过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积.
已知点E(x1,y1)、F(x2,y2)为抛物线y=ax2+bx+c上的两点,过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C,设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积.