题目内容
已知二次函数y=-x2+6x-5的图象与x轴交于点A、B(点A在点B的左侧),顶点为C.
(1)通过配方,确定点C坐标;
(2)二次函数y=x2-2mx+m2-4的图象与x轴交于点D、E(点D在点E的左侧),顶点为F.
①若存在以六点A、B、C、D、E、F中的四点为顶点的四边形为菱形,则m= ;
②是否存在以六点A、B、C、D、E、F中的四点为顶点的四边形为矩形?若存在,求出m 的值;若不存在,请说明理由.
(1)通过配方,确定点C坐标;
(2)二次函数y=x2-2mx+m2-4的图象与x轴交于点D、E(点D在点E的左侧),顶点为F.
①若存在以六点A、B、C、D、E、F中的四点为顶点的四边形为菱形,则m=
②是否存在以六点A、B、C、D、E、F中的四点为顶点的四边形为矩形?若存在,求出m 的值;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)将二次函数配方后即可确定顶点坐标;
(2)A、B、D、E四点在同一直线上,不可能构成四边形,只能四边形ACBF为菱形,点F与点C关于x轴对称,从而确定点F的坐标为(3,-4),然后利用二次函数的对称轴公式求得m的值即可;
(3)A、B、D、E四点在同一直线上,不可能构成四边形,显然,∠ACB≠90°,∠ACB也不可能为矩形的一个内角,所以四边形为矩形的顶点只能是A、C、E、F或B、C、D、F;然后分当以四边形ACEF为矩形时和当四边形BCDF为矩形时两种情况分类讨论即可确定m的值.
(2)A、B、D、E四点在同一直线上,不可能构成四边形,只能四边形ACBF为菱形,点F与点C关于x轴对称,从而确定点F的坐标为(3,-4),然后利用二次函数的对称轴公式求得m的值即可;
(3)A、B、D、E四点在同一直线上,不可能构成四边形,显然,∠ACB≠90°,∠ACB也不可能为矩形的一个内角,所以四边形为矩形的顶点只能是A、C、E、F或B、C、D、F;然后分当以四边形ACEF为矩形时和当四边形BCDF为矩形时两种情况分类讨论即可确定m的值.
解答:解: (1)y=-x2+6x-5=-(x-3)2+4,
(1)y=-x2+6x-5=-(x-3)2+4,
∴点C坐标为(3,4);
(2)①A、B、D、E四点在同一直线上,不可能构成四边形,
∴只能四边形ACBF为菱形,
∴点F与点C关于x轴对称,
∴点F的坐标为(3,-4),
∴二次函数y=x2-2mx+m2-4的顶点为F,
∴-
=3,
解得:m=3;
②A、B、D、E四点在同一直线上,不可能构成四边形,
显然,∠ACB≠90°.
∴∠ACB也不可能为矩形的一个内角;
所以四边形为矩形的顶点只能是A、C、E、F或B、C、D、F.
当以四边形ACEF为矩形时,
函数y=(x-m)2-4的图象可由y=-(x-3)2+4关于x轴的
对称图象沿x轴平移而得,所以△ABC≌△DEF.;
当四边形ACEF为矩形时,△ACG∽△FAH.
∴
=
,
即
=
.
∴AH=8.
∴m=9,
当四边形BCDF为矩形时,同上求得m=-3,
∴当m=-3或9时,存在以六点A、B、C、D、E、F中的四点为顶点的四边形为矩形.
 (1)y=-x2+6x-5=-(x-3)2+4,
(1)y=-x2+6x-5=-(x-3)2+4,∴点C坐标为(3,4);
(2)①A、B、D、E四点在同一直线上,不可能构成四边形,
∴只能四边形ACBF为菱形,
∴点F与点C关于x轴对称,
∴点F的坐标为(3,-4),
∴二次函数y=x2-2mx+m2-4的顶点为F,
∴-
| -2m |
| 2 |
解得:m=3;
②A、B、D、E四点在同一直线上,不可能构成四边形,
显然,∠ACB≠90°.
∴∠ACB也不可能为矩形的一个内角;
所以四边形为矩形的顶点只能是A、C、E、F或B、C、D、F.
当以四边形ACEF为矩形时,
函数y=(x-m)2-4的图象可由y=-(x-3)2+4关于x轴的
对称图象沿x轴平移而得,所以△ABC≌△DEF.;
当四边形ACEF为矩形时,△ACG∽△FAH.
∴
| CG |
| AG |
| AH |
| HF |
即
| 4 |
| 2 |
| AH |
| 4 |
∴AH=8.
∴m=9,
当四边形BCDF为矩形时,同上求得m=-3,
∴当m=-3或9时,存在以六点A、B、C、D、E、F中的四点为顶点的四边形为矩形.
点评:本题考查了二次函数的综合知识,(2)小题中,都用到了分类讨论的数学思想,难点在于考虑问题要全面,做到不重不漏.

练习册系列答案
相关题目
计算2x(3x2+1),正确的结果是( )
| A、5x3+2x |
| B、6x3+1 |
| C、6x3+2x |
| D、6x2+2x |
 如图,?ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.
如图,?ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.
 如图,抛物线y=-
如图,抛物线y=- 如图,AD、BC相交于O,OA=OC,∠OBD=∠ODB.求证:AB=CD.
如图,AD、BC相交于O,OA=OC,∠OBD=∠ODB.求证:AB=CD.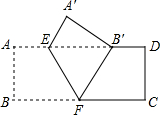 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是