题目内容
如图，?ABCD的对角线AC，BD交于点O，直线EF过点O，分别交AD，BC于点E，F．求证：AE=CF．考点：平行四边形的性质,全等三角形的判定与性质
专题：证明题
分析：利用平行四边形的性质得出AO=CO，AD∥BC，进而得出∠EAC=∠FCO，再利用ASA求出△AOE≌△COF，即可得出答案．
解答：证明：∵?ABCD的对角线AC，BD交于点O，
∴AO=CO，AD∥BC，
∴∠EAC=∠FCO，
在△AOE和△COF中
，
∴△AOE≌△COF（ASA），
∴AE=CF．
∴AO=CO，AD∥BC，
∴∠EAC=∠FCO，
在△AOE和△COF中
|
∴△AOE≌△COF（ASA），
∴AE=CF．
点评：此题主要考查了全等三角形的判定与性质以及平行四边形的性质，熟练掌握全等三角形的判定方法是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
已知甲、乙两地相距90km，A，B两人沿同一公路从甲地出发到乙地，A骑摩托车，B骑电动车，图中DE，OC分别表示A，B离开甲地的路程s（km）与时间t（h）的函数关系的图象，根据图象解答下列问题．下列计算正确的是（ ）
| A、a3÷a2=a | ||
B、
| ||
| C、2a2+a2=3a4 | ||
| D、（a-b）2=a2-b2 |
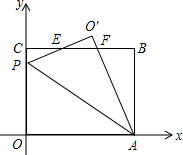在平面直角坐标系中，O是坐标原点，矩形OABC的位置如图所示，点A，C的坐标分别为（10，0），（0，8）．点P是y轴上的一个动点，将△OAP沿AP翻折得到△O′AP，直线BC与直线O′P交于点E，与直线O′A交于点F．