题目内容
 如图,抛物线y=-
如图,抛物线y=-| 1 |
| 2 |
(1)求抛物线的解析式及B点的坐标.
(2)判断△BCD的形状,并说明理由.
(3)若∠BDC=∠PCF,求点P的坐标.
考点:二次函数综合题
专题:
分析:(1)直接利用待定系数法求二次函数解析式得出即可,再利用y=0时,求出图象与x轴交点坐标即可;
(2)首先求出C,D点坐标,再利用勾股定理得出CD,BC,BD的长,进而利用勾股定理逆定理得出△BCD的形状;
(3)根据(2)中所求得出tan∠BDC=tan∠PCF=3,进而求出直线BD的解析式,进而表示出P点坐标,即可代入上式即可.
(2)首先求出C,D点坐标,再利用勾股定理得出CD,BC,BD的长,进而利用勾股定理逆定理得出△BCD的形状;
(3)根据(2)中所求得出tan∠BDC=tan∠PCF=3,进而求出直线BD的解析式,进而表示出P点坐标,即可代入上式即可.
解答: 解:(1)∵抛物线y=-
解:(1)∵抛物线y=-
x2+2x+c与x轴交于点A、B,与y轴交于点C,点A的坐标为(-2,0),
∴0=-
×(-2)2+2×(-2)+c,
解得;c=6,
∴抛物线的解析式为;y=-
x2+2x+6,
当y=0,则0=-
x2+2x+6,
解得:x1=-2,x2=6,
∴B点的坐标为;(6,0);
(2)如图1,过点D作DE⊥x轴于点E,作CN⊥DE于点N,
∵y=-
x2+2x+6,当x=0时,y=6,
∴C(0,6),
∵y=-
x2+2x+6=-
(x-2)2+8,
∴D(2,8),
∴BC=
=6
,CD=
=2
,BD=
=
,
∴BC2+CD2=BD2,
∴△BCD是直角三角形;
(3)如图2,过点P作PN⊥y轴于点N,
∵B((6,0),D(2,8),设直线BD的解析式为:y=kx+b,
则
,
解得:
,
∴直线BD的解析式为:y=-2x+12,
∵∠BDC=∠PCF,
∴tan∠BDC=tan∠PCF=
=
=
=3,
设P点坐标为:(x,-2x+12),
∴NC=NO-CO=-2x+12-6=-2x+6,
NP=x,
∴
=3,
解得;x=
,
经检验得出:x=
是原方程的根,
∴-2x+12=-2×
=12=
,
∴P(
,
).
 解:(1)∵抛物线y=-
解:(1)∵抛物线y=-| 1 |
| 2 |
∴0=-
| 1 |
| 2 |
解得;c=6,
∴抛物线的解析式为;y=-
| 1 |
| 2 |
当y=0,则0=-
| 1 |
| 2 |
解得:x1=-2,x2=6,
∴B点的坐标为;(6,0);
(2)如图1,过点D作DE⊥x轴于点E,作CN⊥DE于点N,
∵y=-
| 1 |
| 2 |
∴C(0,6),
∵y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴D(2,8),
∴BC=
| 62+62 |
| 2 |
| CN2+DN2 |
| 2 |
| ED2+BE2 |
| 80 |
∴BC2+CD2=BD2,
∴△BCD是直角三角形;
(3)如图2,过点P作PN⊥y轴于点N,
∵B((6,0),D(2,8),设直线BD的解析式为:y=kx+b,
则
|
解得:
|

∴直线BD的解析式为:y=-2x+12,
∵∠BDC=∠PCF,
∴tan∠BDC=tan∠PCF=
| BC |
| CD |
| PN |
| NC |
6
| ||
2
|
设P点坐标为:(x,-2x+12),
∴NC=NO-CO=-2x+12-6=-2x+6,
NP=x,
∴
| x |
| -2x+6 |
解得;x=
| 18 |
| 7 |
经检验得出:x=
| 18 |
| 7 |
∴-2x+12=-2×
| 18 |
| 7 |
| 48 |
| 7 |
∴P(
| 18 |
| 7 |
| 48 |
| 7 |
点评:此题主要考查了二次函数综合以及勾股定理以及逆定理和待定系数法求一次函数解析式等知识,利用图象上点的坐标性质表示出P点坐标是解题关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
下列计算正确的是( )
| A、a3÷a2=a | ||
B、
| ||
| C、2a2+a2=3a4 | ||
| D、(a-b)2=a2-b2 |
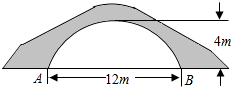 如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=-
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=- 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.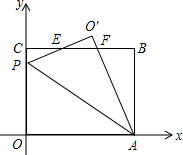 在平面直角坐标系中,O是坐标原点,矩形OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8).点P是y轴上的一个动点,将△OAP沿AP翻折得到△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.
在平面直角坐标系中,O是坐标原点,矩形OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8).点P是y轴上的一个动点,将△OAP沿AP翻折得到△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.