题目内容
 如图,OE平分∠AOB,OD平分∠AOC,∠DOE=40°,求∠BOC的度数.
如图,OE平分∠AOB,OD平分∠AOC,∠DOE=40°,求∠BOC的度数.考点:角平分线的定义
专题:
分析:设∠DOC=x,∠COE=y.根据角平分线定义及角的和差得出∠BOE=∠AOE=2x+y,那么∠BOC=∠BOE+∠COE=2x+2y.由∠DOE=40°,得到x+y=40°,于是∠BOC=2x+2y=80°.
解答:解:设∠DOC=x,∠COE=y.
∵OD平分∠AOC,
∴∠AOC=2∠DOC=2x,
∴∠AOE=∠AOC+∠COE=2x+y,
∵OE平分∠AOB,
∴∠BOE=∠AOE=2x+y,
∴∠BOC=∠BOE+∠COE=2x+y+y=2x+2y.
∵∠DOE=40°,
∴x+y=40°,
∴∠BOC=2x+2y=80°.
∵OD平分∠AOC,
∴∠AOC=2∠DOC=2x,
∴∠AOE=∠AOC+∠COE=2x+y,
∵OE平分∠AOB,
∴∠BOE=∠AOE=2x+y,
∴∠BOC=∠BOE+∠COE=2x+y+y=2x+2y.
∵∠DOE=40°,
∴x+y=40°,
∴∠BOC=2x+2y=80°.
点评:本题考查了角平分线定义和角的有关计算的应用,主要考查学生计算能力和推理能力,设出辅助未知数x与y可以提高解题速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,五边形ABCDE为正五边形,以下结论正确的是( )
如图,五边形ABCDE为正五边形,以下结论正确的是( )| A、它的内角和为900° |
| B、它的外角和为540° |
| C、它共有两条对角线 |
| D、它共用五条对称轴 |
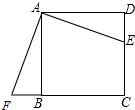 如图,在边长为6的正方形ABCD中,E是CD上一点,F在CB的延长线上,且DE=BF.
如图,在边长为6的正方形ABCD中,E是CD上一点,F在CB的延长线上,且DE=BF. 如图,请把△ABC和△A′B′C′图形补充完整,使得它们关于直线l对称.(保留作图痕迹)
如图,请把△ABC和△A′B′C′图形补充完整,使得它们关于直线l对称.(保留作图痕迹)
 在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=
在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=
 某种药物有三种不同的配方,如图,三条抛物线表示这三种配方在给药量相同的情况下,每毫升血液中的含药量y(微克)随时间x(小时)的变化情况,这种药物每毫升血液中的含药量大于9微克,则会发生中毒,小于5微克,则没有疗效.
某种药物有三种不同的配方,如图,三条抛物线表示这三种配方在给药量相同的情况下,每毫升血液中的含药量y(微克)随时间x(小时)的变化情况,这种药物每毫升血液中的含药量大于9微克,则会发生中毒,小于5微克,则没有疗效.