题目内容
若四边形ABCD的对角线AC与BD相交于点O,且OA=OB=OC=OD=
AB,则四边形ABCD是正方形吗?请说明理由.
| ||
| 2 |
考点:正方形的判定
专题:
分析:根据平行四边形的判定推出四边形是平行四边形,求出AC=BD,得出四边形是矩形,根据勾股定理的逆定理求出AC⊥BD,根据正方形的判定推出即可.
解答:解:四边形ABCD是正方形,
理由是: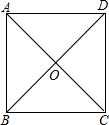 ∵OA=OB=OC=OD,
∵OA=OB=OC=OD,
∴AC=BD,四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形,
∵OA=OB=OC=OD=
AB,
∴OA2+OB2=AB2,
∴∠AOB=90°,
即AC⊥BD,
∴四边形ABCD是正方形.
理由是:
 ∵OA=OB=OC=OD,
∵OA=OB=OC=OD,∴AC=BD,四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形,
∵OA=OB=OC=OD=
| ||
| 2 |
∴OA2+OB2=AB2,
∴∠AOB=90°,
即AC⊥BD,
∴四边形ABCD是正方形.
点评:本题考查了勾股定理的逆定理,平行四边形的判定,矩形的判定,正方形的判定的应用,主要考查学生的推理能力,注意:对角线互相垂直的矩形是正方形,难度适中.

练习册系列答案
相关题目
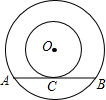 如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )
如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )| A、2cm | B、4cm |
| C、8cm | D、16cm |
 如图,OE平分∠AOB,OD平分∠AOC,∠DOE=40°,求∠BOC的度数.
如图,OE平分∠AOB,OD平分∠AOC,∠DOE=40°,求∠BOC的度数. 如图,在⊙O中,C为弦AB上一点,AC=2,BC=6,⊙O的半径为5,则OC=
如图,在⊙O中,C为弦AB上一点,AC=2,BC=6,⊙O的半径为5,则OC= 如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度.
如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度.