题目内容
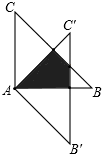 如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=
如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=| 2 |
考点:旋转的性质,等腰直角三角形
专题:压轴题
分析:根据题意结合旋转的性质以及等腰直角三角形的性质得出AD=
BC=1,AF=FC′=
AC′=1,进而求出阴影部分的面积.
| 1 |
| 2 |
| ||
| 2 |
解答: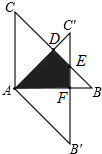 解:∵△ABC绕点A顺时针旋转45°得到△A′B′C′,∠BAC=90°,AB=AC=
解:∵△ABC绕点A顺时针旋转45°得到△A′B′C′,∠BAC=90°,AB=AC=
,
∴BC=2,∠C=∠B=∠CAC′=∠C′=45°,
∴AD⊥BC,B′C′⊥AB,
∴AD=
BC=1,AF=FC′=
AC′=1,
∴图中阴影部分的面积等于:S△AFC′-S△DEC′=
×1×1-
×(
-1)2=
-1.
故答案为:
-1.
 解:∵△ABC绕点A顺时针旋转45°得到△A′B′C′,∠BAC=90°,AB=AC=
解:∵△ABC绕点A顺时针旋转45°得到△A′B′C′,∠BAC=90°,AB=AC=| 2 |
∴BC=2,∠C=∠B=∠CAC′=∠C′=45°,
∴AD⊥BC,B′C′⊥AB,
∴AD=
| 1 |
| 2 |
| ||
| 2 |
∴图中阴影部分的面积等于:S△AFC′-S△DEC′=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:
| 2 |
点评:此题主要考查了旋转的性质以及等腰直角三角形的性质等知识,得出AD,AF,DC′的长是解题关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
在一次中学生田径运动会上,参加跳高的15名运动员的成绩如表:
那么这些运动员跳高成绩的众数是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
| A、4 | B、1.75 |
| C、1.70 | D、1.65 |
 将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的一半(木条宽度忽略不计),则这个平行四边形的最小内角为
将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的一半(木条宽度忽略不计),则这个平行四边形的最小内角为