题目内容
若|x+1|=-1-x,|3x+4|=3x+4,则x的取值范围为 .
考点:解一元一次不等式组,绝对值
专题:
分析:先根据绝对值的性质得出关于x的不等式组,求出x的取值范围即可.
解答:解:∵|x+1|=-1-x,|3x+4|=3x+4,
∴
,
由①得,x≤-1,
由②得,x≥-
,
∴x的取值范围为:-
≤x≤-1.
故答案为:-
≤x≤-1.
∴
|
由①得,x≤-1,
由②得,x≥-
| 4 |
| 3 |
∴x的取值范围为:-
| 4 |
| 3 |
故答案为:-
| 4 |
| 3 |
点评:本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
在同一平面内,从①AB∥CD,②BC∥AD,③AB=CD,④BC=AD.这四个条件中任选两个能使四边形ABCD是平行四边形的选法有( )
| A、3 种 | B、4种 |
| C、5种 | D、6种 |
要求画△ABC的边AB上的高,下列画法中,正确的是( )
A、 |
B、 |
C、 |
D、 |
在实数:3.14159,
,1.010010001…,4.
,π,
,
中,无理数有( )
| 3 | 64 |
| •• |
| 21 |
| 3 |
| 22 |
| 7 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=4.
在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=4.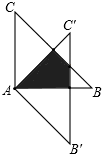 如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=
如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=