题目内容
已知直线L:y=3x+2,现有下列命题:
①过点P(-1,1)与直线L平行的直线是y=3x+4;
②若直线L与x轴、y轴分别交于A、B两点,则AB=
;
③若点M(-
,1),N(a,b)都在直线L上,且a>-
,则b>1;
④若点Q到两坐标轴的距离相等,且Q在L上,则点Q在第一或第二象限.
其中正确的命题是 .
①过点P(-1,1)与直线L平行的直线是y=3x+4;
②若直线L与x轴、y轴分别交于A、B两点,则AB=
| 2 |
| 3 |
| 10 |
③若点M(-
| 1 |
| 3 |
| 1 |
| 3 |
④若点Q到两坐标轴的距离相等,且Q在L上,则点Q在第一或第二象限.
其中正确的命题是
考点:命题与定理,一次函数的性质
专题:
分析:由于k相等,且P点在直线t=3x+4上,则可判断①正确;先确定A点和B点坐标,再利用两点间的距离公式计算AB,则可对②进行判断;根据一次函数的性质对③进行判断;根据两直线的交点问题解有y=3x+2与y=x或y=-x所组成的方程,确定Q点的坐标,则可对④进行判断.
解答:解:当x=-1时,y=3x+4=-3+4=1,则过点P(-1,1)与直线L平行的直线是y=3x+4,所以①正确;
A点坐标为(-
,0),B点坐标为(0,2),则AB=
=
,所以②正确;
由于k=3>0,y随x的增大而增大,则a>-
,则b>1,所以③正确;
解方程组
得
,解方程组
得
,即Q点的坐标为(-1,-1)或(-
,
),所以④错误.
故答案为①②③.
A点坐标为(-
| 2 |
| 3 |
(
|
2
| ||
| 3 |
由于k=3>0,y随x的增大而增大,则a>-
| 1 |
| 3 |
解方程组
|
|
|
|
| 1 |
| 2 |
| 1 |
| 2 |
故答案为①②③.
点评:本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.也考查了一次函数的性质.

练习册系列答案
相关题目
在同一平面内,从①AB∥CD,②BC∥AD,③AB=CD,④BC=AD.这四个条件中任选两个能使四边形ABCD是平行四边形的选法有( )
| A、3 种 | B、4种 |
| C、5种 | D、6种 |
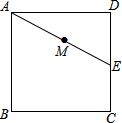 如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于
如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于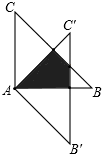 如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=
如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=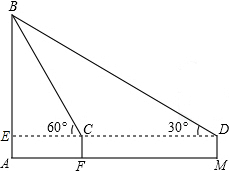 如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取
如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取