题目内容
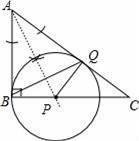
如图,△ABC中,∠ABC=90°.
(1)请在BC上找一点P,作⊙P与AC,AB都相切,切点为Q;(尺规作图,保留作图痕迹)
(2)若AB=3,BC=4,求第(1)题中所作圆的半径;
(3)连结BQ,第(2)中的条件均不变,求sin∠CBQ.


【考点】作图—复杂作图;切线的性质;相似三角形的判定与性质.
【专题】作图题.
【分析】(1)作∠BAC的平分线交BC于P点,然后以点P为圆心,PB为半径作圆即可;
(2)连结PQ,如图,先计算出AC=5,设半径为r,BP=PQ=r,PC=4﹣r,再证明Rt△CPQ∽Rt△CAB,则可利用相似比计算出r即可;
(3)先利用切线长定理得到AB=AQ,加上PB=PQ,则判定AP为BQ的垂直平分线,则利用等角的余角相等得到∠CBQ=∠BAP,然后在Rt△ABP中利用正弦定义求出sin∠BAP,从而可得到sin∠CBQ的值.
【解答】解:(1)如图,⊙P为所作;
(2)连结PQ,如图,
在Rt△ABC中,AC=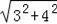
 =5,
=5,
设半径为r,BP=PQ=r,PC=4﹣r
∵AB与⊙P相切于Q,
∴PQ⊥AC,
∵∠PCQ=∠ACP,
∴Rt△CPQ∽Rt△CAB,
∴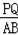
 =
=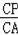
 ,即
,即
 =
=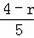
 ,解得r=
,解得r=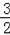
 ,
,
即所作圆的半径为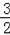
 ;
;
(3)∵AB、AQ为⊙P的切线,
∴AB=AQ,
∵PB=PQ,
∴AP为BQ的垂直平分线,
∴∠BAP+∠ABQ=90°,
∵∠CBQ+∠ABQ=90°,
∴∠CBQ=∠BAP,
在Rt△ABP中,AP=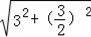
 =
=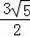
 ,
,
∴sin∠BAP=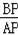
 =
=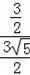
 =
=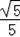
 ,
,
∴sin∠CBQ=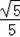
 .
.

【点评】本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了勾股定理、相似三角形的判定与性质和三角函数的定义.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案2001年亚洲铁人三项赛在徐州市风光秀丽的云龙湖畔举行.比赛程序是:运动员先同时下水游泳1.5千米到第一换项点,在第一换项点整理服装后,接着骑自行车行40千米到第二换项点,再跑步10千米到终点.下表是2001年亚洲铁人三项赛女子组(19岁以下)三名运动员在比赛中的成绩(游泳成绩即游泳所用时间,其它类推,表内时间单位为秒)
| 运动员号码 | 游泳成绩 | 第一换项点所用时间 | 自行车成绩 | 第二换项点所用时间 | 长跑成绩 |
| 191 | 1997 | 75 | 4927 | 40 | 3220 |
| 194 | 1503 | 110 | 5686 | 57 | 3652 |
| 195 | 1354 | 74 | 5351 | 44 | 3195 |
(1)填空(精确到0.01):
第191号运动员骑自行车的平均速度是 米/秒;
第194号运动员骑自行车的平均速度是 米/秒;
第195号运动员骑自行车的平均速度是 米/秒;
(2)如果运动员骑自行车都是匀速的,那么在骑自行车的途中,191号运动员会追上195号或194号吗?如果会,那么追上时离第一换项点有多少米(精确到0.01)?如果不会,为什么?
(3)如果长跑也都是匀速的,那么在长跑途中这三名运动员中有可能某人追上某人吗?为什么?



 B.
B.

 )的下方,那么m的取值范围是( )
)的下方,那么m的取值范围是( )
 B.
B.
 C.
C.



 B.
B.
 C.
C.
 D.
D.



 的值。
的值。 =
=
 的值。
的值。