题目内容
11.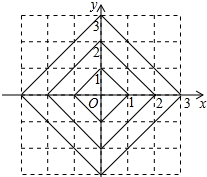 如图,在平面直角坐标系中,横、纵坐标都为整数的点称为整点,观察图中每一个正方形(实线)四条边上的整点的个数.则由里向外的第四个正方形上有16个整点,第n个正方形上有4n个整点.
如图,在平面直角坐标系中,横、纵坐标都为整数的点称为整点,观察图中每一个正方形(实线)四条边上的整点的个数.则由里向外的第四个正方形上有16个整点,第n个正方形上有4n个整点.
分析 根据整点的定义,可以发现第1个正方形的整点有4个,第2个正方形有8个,第3个正方形有12个,则第4个有16个,故第n个有4n个整点.
解答 解:∵第1个正方形有4×1=4个整点,
第2个正方形有4×2=8个整点,
第3个正方形有4×3=12个整点,
∴第4个正方形有4×4=16个整点,
∴第n个正方形上有4n个整点,
故答案为:16,4n.
点评 本题主要考查点的坐标规律、正方形各边相等的性质,解决本题的关键是观察分析,得到规律是解答此题的关键.

练习册系列答案
相关题目
1.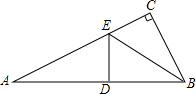 如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )
如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )
 如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )
如图,在△ABC中,∠C=90°,沿过点B的一条直线BE,折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 45° |
20.使分式$\frac{2x+1}{2x-1}$无意义的x的值是( )
| A. | x≠-$\frac{1}{2}$ | B. | x≠$\frac{1}{2}$ | C. | x=$\frac{1}{2}$ | D. | x=-$\frac{1}{2}$ |
1.数据6,7,5,7,6,13,5,6,8的众数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 5或6或7 |
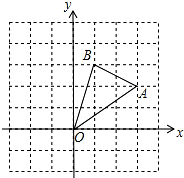 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).将△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).将△AOB绕点O逆时针旋转90°后得到△A1OB1. 作图题:
作图题: