题目内容
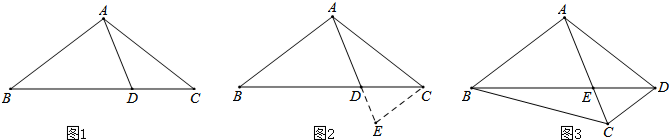
2.阅读下面材料:小明遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.
小明发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图2).
(1)请回答:∠ACE的度数为75°,AC的长为3.
(2)参考小明思考问题的方法,解决问题:
如图3,在四边形ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求AC的长.
分析 根据相似的三角形的判定与性质,可得$\frac{AB}{DF}$=$\frac{AE}{EF}$=$\frac{BE}{DE}$=2,根据等腰三角形的判定,可得AE=AC,根据正切函数,可得DF的长,根据直角三角形的性质,可得AB与DF的关系,根据勾股定理,可得答案.
解答 解:∠ACE=75°,AC的长为3.
过点D作DF⊥AC于点F.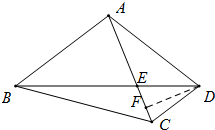
∵∠BAC=90°=∠DFA,
∴AB∥DF,
∴△ABE∽△FDE,
∴$\frac{AB}{DF}$=$\frac{AE}{EF}$=$\frac{BE}{DE}$=2,
∴EF=1,AB=2DF.
在△ACD中,∠CAD=30°,∠ADC=75°,
∴∠ACD=75°,AC=AD.
∵DF⊥AC,
∴∠AFD=90°,
在△AFD中,AF=2+1=3,∠FAD=30°,
∴DF=AFtan30°=$\sqrt{3}$,AD=2DF=2$\sqrt{3}$.
∴AC=AD=2$\sqrt{3}$.
点评 本题考查了相似三角形的判定与性质,利用了相似三角形的判定与性质,直角三角形的性质,勾股定理.

练习册系列答案
相关题目
14.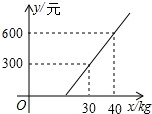 国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )
国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )
 国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )
国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )| A. | 20kg | B. | 25kg | C. | 28kg | D. | 30kg |
12.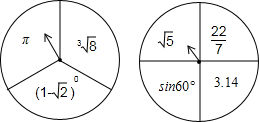 如图所示的两个转盘分别被均匀地分成3个和4个扇形如图所示的两个转盘分别被均匀地分成3个和4个扇形,每个扇形上都标有一个实数.同时自由转动两个转盘,转盘停止后(若指针指在分格线上,则重转),两个指针都落在无理数上的概率是( )
如图所示的两个转盘分别被均匀地分成3个和4个扇形如图所示的两个转盘分别被均匀地分成3个和4个扇形,每个扇形上都标有一个实数.同时自由转动两个转盘,转盘停止后(若指针指在分格线上,则重转),两个指针都落在无理数上的概率是( )
 如图所示的两个转盘分别被均匀地分成3个和4个扇形如图所示的两个转盘分别被均匀地分成3个和4个扇形,每个扇形上都标有一个实数.同时自由转动两个转盘,转盘停止后(若指针指在分格线上,则重转),两个指针都落在无理数上的概率是( )
如图所示的两个转盘分别被均匀地分成3个和4个扇形如图所示的两个转盘分别被均匀地分成3个和4个扇形,每个扇形上都标有一个实数.同时自由转动两个转盘,转盘停止后(若指针指在分格线上,则重转),两个指针都落在无理数上的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
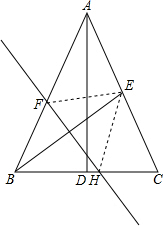 如图,在△ABC中,AB=AC,底边BC上的高AD=12,tan C=2,如果将△ABC沿直线l翻折后,点B刚好落在AC边的中点E处,直线l与边AB交于点F,与边BC交于点H,求BH的长.
如图,在△ABC中,AB=AC,底边BC上的高AD=12,tan C=2,如果将△ABC沿直线l翻折后,点B刚好落在AC边的中点E处,直线l与边AB交于点F,与边BC交于点H,求BH的长.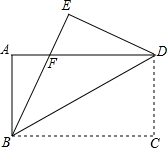 如图,沿矩形ABCD的对角线BD折叠,点C落在点E的位置,已知BC=8cm,AB=6cm,那么折叠后的重合部分的面积是多少?
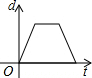
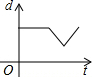
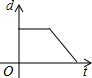
如图,沿矩形ABCD的对角线BD折叠,点C落在点E的位置,已知BC=8cm,AB=6cm,那么折叠后的重合部分的面积是多少?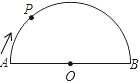 如图,在直径为AB的半圆O上有一动点P从O点出发,以相同的速度沿O-A-B-O的路线运动,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )
如图,在直径为AB的半圆O上有一动点P从O点出发,以相同的速度沿O-A-B-O的路线运动,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )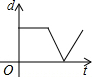
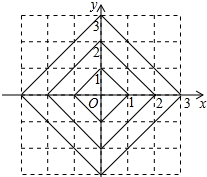 如图,在平面直角坐标系中,横、纵坐标都为整数的点称为整点,观察图中每一个正方形(实线)四条边上的整点的个数.则由里向外的第四个正方形上有16个整点,第n个正方形上有4n个整点.
如图,在平面直角坐标系中,横、纵坐标都为整数的点称为整点,观察图中每一个正方形(实线)四条边上的整点的个数.则由里向外的第四个正方形上有16个整点,第n个正方形上有4n个整点.