题目内容
6.平面直角坐标系中,点P(3,-2)关于点(1,0)对称的点的坐标是(-1,2).分析 设A(1,0),连结PA并延长到点P′,使P′A=PA,设P′(x,y),则x<0,y>0.过P作PM⊥x轴于点M,过P′作PN⊥x轴于点N.利用AAS证明△AP′N≌△APM,得出AN=AM,P′N=PM,即1-x=3-1,y=2,求出x=-1,y=2,进而得到P′的坐标.
解答 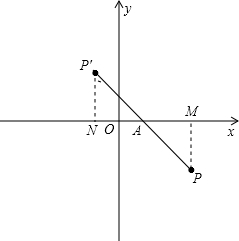 解:如图,设A(1,0),连结PA并延长到点P′,使P′A=PA,设P′(x,y),则x<0,y>0.
解:如图,设A(1,0),连结PA并延长到点P′,使P′A=PA,设P′(x,y),则x<0,y>0.
过P作PM⊥x轴于点M,过P′作PN⊥x轴于点N.
在△AP′N与△APM中,
$\left\{\begin{array}{l}{∠ANP′=∠AMP}\\{∠NAP′=∠MAP}\\{AP′=AP}\end{array}\right.$,
∴△AP′N≌△APM(AAS),
∴AN=AM,P′N=PM,
∴1-x=3-1,y=2,
∴x=-1,y=2,
∴P′(-1,2).
故答案为(-1,2).
点评 本题考查了坐标与图形变化-旋转,全等三角形的判定与性质,准确作出点P(3,-2)关于点(1,0)对称的点P′是解题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
14.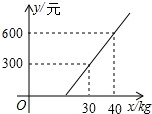 国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )
国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )
 国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )
国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )| A. | 20kg | B. | 25kg | C. | 28kg | D. | 30kg |
15.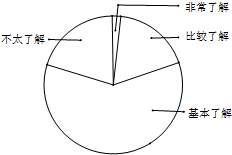 玉环县某学校数学兴趣小组在本校学生中开展主题为“五水共治”的专题调查活动,采取随机抽样的方法进行问卷调查.问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如表:
玉环县某学校数学兴趣小组在本校学生中开展主题为“五水共治”的专题调查活动,采取随机抽样的方法进行问卷调查.问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如表:
(1)本次调查抽取的样本容量是多少?表中m的值为多少?
(2)根据表中数据计算等级为“比较了解”的频数在扇形统计图中所对应的扇形圆心角的度数,并补全扇形统计图;
(3)若该校有1500名学生,请根据调查结果,估计这些学生中对五水共治“比较了解”的人数大约有多少?
 玉环县某学校数学兴趣小组在本校学生中开展主题为“五水共治”的专题调查活动,采取随机抽样的方法进行问卷调查.问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如表:
玉环县某学校数学兴趣小组在本校学生中开展主题为“五水共治”的专题调查活动,采取随机抽样的方法进行问卷调查.问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如表:| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 4 | 36 | 120 | 40 |
| 频率 | 0.02 | 0.18 | m | 0.2 |
(2)根据表中数据计算等级为“比较了解”的频数在扇形统计图中所对应的扇形圆心角的度数,并补全扇形统计图;
(3)若该校有1500名学生,请根据调查结果,估计这些学生中对五水共治“比较了解”的人数大约有多少?
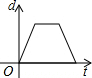
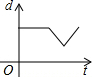
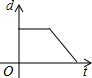
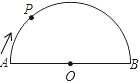 如图,在直径为AB的半圆O上有一动点P从O点出发,以相同的速度沿O-A-B-O的路线运动,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )
如图,在直径为AB的半圆O上有一动点P从O点出发,以相同的速度沿O-A-B-O的路线运动,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )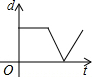
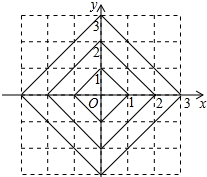 如图,在平面直角坐标系中,横、纵坐标都为整数的点称为整点,观察图中每一个正方形(实线)四条边上的整点的个数.则由里向外的第四个正方形上有16个整点,第n个正方形上有4n个整点.
如图,在平面直角坐标系中,横、纵坐标都为整数的点称为整点,观察图中每一个正方形(实线)四条边上的整点的个数.则由里向外的第四个正方形上有16个整点,第n个正方形上有4n个整点. 如图,点A在反比例函数y=$\frac{4}{x}$的图象上,点B在反比例函数y=$\frac{k}{x}$(k<0)的图象上,且∠AOB=90°,tan∠OAB=$\frac{4}{3}$,则k的值是-$\frac{16}{9}$.
如图,点A在反比例函数y=$\frac{4}{x}$的图象上,点B在反比例函数y=$\frac{k}{x}$(k<0)的图象上,且∠AOB=90°,tan∠OAB=$\frac{4}{3}$,则k的值是-$\frac{16}{9}$.