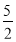题目内容
已知二次函数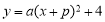 的图象是由函数
的图象是由函数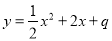 的图象向左平移一个单位得到.反比例函数
的图象向左平移一个单位得到.反比例函数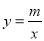 与二次函数
与二次函数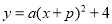 的图象交于点A(1,n).
的图象交于点A(1,n).
(1)求a,p,q,m,n的值;
(2)要使反比例函数和二次函数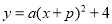 在直线
在直线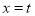 的一侧都是y随着x的增大而减小,求t的最大值;
的一侧都是y随着x的增大而减小,求t的最大值;
(3)记二次函数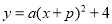 图象的顶点为B,以AB为边构造矩形ABCD,边CD与函数
图象的顶点为B,以AB为边构造矩形ABCD,边CD与函数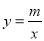 相交,且直线AB与CD的距离为
相交,且直线AB与CD的距离为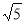 ,求出点D,C的坐标.
,求出点D,C的坐标.
(1)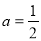 ,p=3,q=6,m=12,n=12;(2)-3;(3)D的坐标为(3,11),点C(﹣1,3).
,p=3,q=6,m=12,n=12;(2)-3;(3)D的坐标为(3,11),点C(﹣1,3).
【解析】
试题分析:(1)先将函数y=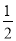 x2+2x+q配方,即可得到顶点坐标(-2,q-2),根据平移的性质可得a=
x2+2x+q配方,即可得到顶点坐标(-2,q-2),根据平移的性质可得a=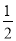 ,p=3,q=6,再把x=1,y=n代入y=
,p=3,q=6,再把x=1,y=n代入y=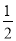 (x+3)2+4,把x=1,y=12代入y=
(x+3)2+4,把x=1,y=12代入y=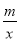 可求m,n的值;
可求m,n的值;
(2)根据反比例函数的增减性,二次函数y=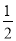 (x+3)2+4的对称轴和增减性,即可求得t的最大值;
(x+3)2+4的对称轴和增减性,即可求得t的最大值;
(3)过点A作直线l∥x轴,作DF⊥l于F,BE⊥l于E.,根据勾股定理,矩形的性质,相似三角形的判定和性质,即可求得点D,C的坐标.
试题解析:【解析】
(1)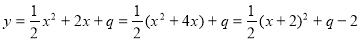 ,顶点坐标(﹣2,q﹣2)
,顶点坐标(﹣2,q﹣2)
(或用顶点坐标公式)
∴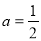 ,p=3,q=6,
,p=3,q=6,
把x=1,y=n代入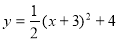 得n=12;
得n=12;
把x=1,y=12代入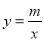 得m=12;
得m=12;
(2)∵反比例函数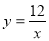 在图象所在的每一象限内,y随着x的增大而减小
在图象所在的每一象限内,y随着x的增大而减小
而二次函数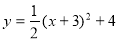 的对称轴为:直线x=﹣3
的对称轴为:直线x=﹣3
要使二次函数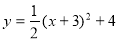 满足上述条件,x≤﹣3
满足上述条件,x≤﹣3
∴t的最大值为﹣3;
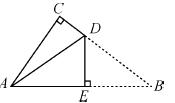
(3)如图,过点A作直线l∥x轴,作DF⊥l于F,BE⊥l于E.
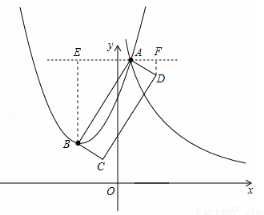
∵点B的坐标为(﹣3,4),A(1,12)
∴AE=4,BE=8
∵BE⊥l,
∴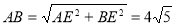
∵四边形ABCD是矩形,
∴∠BAD=90°,∴∠EAB+∠FAD=90°
∵BE⊥l于E,
∴∠EAB+∠EBA=90°∴∠FAD=∠EBA
∴Rt△EBA∽Rt△FAD∴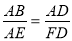
又∵AD=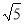 ,
,
∴FD=1
同理:AF=2
∴点D的坐标为(3,11)
同理可求点C(﹣1,3).
考点:二次函数综合题.

 备战中考寒假系列答案
备战中考寒假系列答案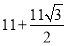
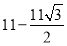
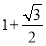
 ,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )