题目内容
在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC= ;S△DEF:S△ADE = 。
1:2.1:3.
【解析】
试题分析:证明△DFE∽△BAE,然后利用对应边成比例,E为OD的中点,求出DF:AB的值,又知AB=DC,即可得出DF:FC的值.过E作EM⊥CD,反向延长交AB于点N,根据△DEF∽△BEA,即可求得ME与MN的比值,则△DEF和△DAF的面积即可求解,进而求得所求.
试题解析:在平行四边形ABCD中,AB∥DC,

则△DFE∽△BAE,
∴ ,
,
∵O为对角线的交点,
∴DO=BO,
又∵E为OD的中点,
∴DE= DB,
DB,
则DE:EB=1:3,
∴DF:AB=1:3,
∵DC=AB,
∴DF:DC=1:3,
∴DF:FC=1:2.
过E作EM⊥CD,反向延长交AB于点N,

∵平行四边形ABCD中,OB=OD,E为OD的中点,
∴BE=3DE,CD∥AB,
∴△DEF∽△BEA,
∴ ,
,
∴ ,
,
∴ ,
,
∴S△DEF:S△ADE=1:3.
考点:1.相似三角形的判定与性质;2.平行四边形的性质.

练习册系列答案
相关题目

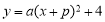 的图象是由函数
的图象是由函数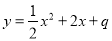 的图象向左平移一个单位得到.反比例函数
的图象向左平移一个单位得到.反比例函数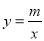 与二次函数
与二次函数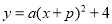 的图象交于点A(1,n).
的图象交于点A(1,n).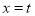 的一侧都是y随着x的增大而减小,求t的最大值;
的一侧都是y随着x的增大而减小,求t的最大值;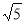 ,求出点D,C的坐标.
,求出点D,C的坐标.

 B.
B. C.
C. D.
D.
 有最小值-3,则
有最小值-3,则 等于( )
等于( ) C.±1 D.
C.±1 D.

 B.
B. C.
C. D.0
D.0