题目内容
如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.
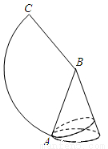
(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度.
(1) ,120°;(2)
,120°;(2) .
.
【解析】
试题分析:(1)根据勾股定理直接求出圆锥的高,再利用圆锥侧面展开图弧长与其底面周长的长度关系,求出侧面展开图中∠ABC的度数即可;
(2)首先求出BD的长,再利用勾股定理求出AD以及AC的长即可.
试题解析:(1)圆锥的高= =
= ,
,
底面圆的周长等于:2π×2= ,
,
解得:n=120°;
(2)连结AC,过B作BD⊥AC于D,则∠ABD=60°.

由AB=6,可求得BD=3,
∴AD═ ,
,
AC=2AD= ,
,
即这根绳子的最短长度是 .
.
考点:1.圆锥的计算;2.勾股定理;3.平面展开-最短路径问题.

练习册系列答案
相关题目



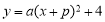 的图象是由函数
的图象是由函数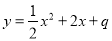 的图象向左平移一个单位得到.反比例函数
的图象向左平移一个单位得到.反比例函数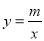 与二次函数
与二次函数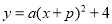 的图象交于点A(1,n).
的图象交于点A(1,n).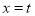 的一侧都是y随着x的增大而减小,求t的最大值;
的一侧都是y随着x的增大而减小,求t的最大值;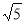 ,求出点D,C的坐标.
,求出点D,C的坐标.

 B.
B. C.
C. D.
D.
 中,AB是⊙O的直径,⊙O与AC交于点D,
中,AB是⊙O的直径,⊙O与AC交于点D, ,求
,求 的度数;
的度数;