题目内容
8. 如图所示,已知∠1=∠2,∠C=∠F,请问直线DF与直线AC存在怎样的位置关系?并说明理由.
如图所示,已知∠1=∠2,∠C=∠F,请问直线DF与直线AC存在怎样的位置关系?并说明理由.
分析 先由对顶角相等可得:∠2=∠3,然后由∠1=∠2,根据等量代换可得:∠1=∠3,然后由同位角相等两直线平行可得:FB∥EC,然后由两直线平行同位角相等可得∠FBA=∠C,然后由∠C=∠F,根据等量代换可得:∠FBA=∠F,然后根据内错角相等两直线平行,即可说明直线DF与直线AC平行.
解答 解:直线DF与直线AC平行,
理由:如图所示,
∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴FB∥EC,
∴∠FBA=∠C,
∵∠C=∠F,
∴∠FBA=∠F,
∴DF∥AC.
∴直线DF与直线AC平行.
点评 此题考查了平行线的判定与性质,解题的关键是:熟记同位角相等?两直线平行,内错角相等?两直线平行,同旁内角互补?两直线平行.

练习册系列答案
相关题目
18.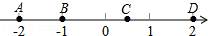 如图,数轴上有A,B,C,D四个点,其中到原点距离相等的两个点是( )
如图,数轴上有A,B,C,D四个点,其中到原点距离相等的两个点是( )
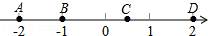 如图,数轴上有A,B,C,D四个点,其中到原点距离相等的两个点是( )
如图,数轴上有A,B,C,D四个点,其中到原点距离相等的两个点是( )| A. | 点B与点D | B. | 点A与点C | C. | 点A与点D | D. | 点B与点C |
16.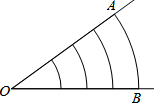 某中学的铅球场地如图所示,已知半径OA=10米,$\widehat{AB}$=2π米,则扇形OAB的面积为( )
某中学的铅球场地如图所示,已知半径OA=10米,$\widehat{AB}$=2π米,则扇形OAB的面积为( )
 某中学的铅球场地如图所示,已知半径OA=10米,$\widehat{AB}$=2π米,则扇形OAB的面积为( )
某中学的铅球场地如图所示,已知半径OA=10米,$\widehat{AB}$=2π米,则扇形OAB的面积为( )| A. | π平方米 | B. | 5π平方米 | C. | 10π平方米 | D. | 20π平方米 |
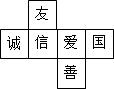 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“友”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“友”相对的面上的汉字是( )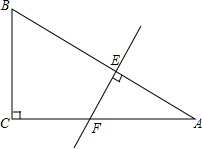 如图,在△ABC中,∠C=90°,∠A=22.5°,AB的垂直平分线交AC于F,交AB于E,若CF=3cm,求BC的长.
如图,在△ABC中,∠C=90°,∠A=22.5°,AB的垂直平分线交AC于F,交AB于E,若CF=3cm,求BC的长.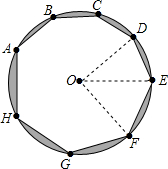 同圆或等圆中,圆心角互余的两个扇形叫做互余共轭扇形.如图⊙O内接八边形中,已知AB=BC=CD=DE=2,EF=FG=GH=HA=2$\sqrt{2}$.
同圆或等圆中,圆心角互余的两个扇形叫做互余共轭扇形.如图⊙O内接八边形中,已知AB=BC=CD=DE=2,EF=FG=GH=HA=2$\sqrt{2}$.